Този метод не е ограничение на дясната ръка на (1) или (4), в допълнение към условията на съществуване и уникалността на решения. Тя може да се използва за изследване на стабилността на движението на всяка система от диференциални уравнения, но, за съжаление, до този момент не е развита общ метод за изграждане на Ляпунов функции, необходими за да се отговори на стабилността на движение на нелинейни системи.
В изследване на стабилността на движението на нелинейни системи от тип (1), този метод също така счита система от диференциални уравнения в отклонения (4). Задачата е да се определят условията за функцията вектор. в която положението на равновесие на системата е асимптотично стабилна. Както е отбелязано по-горе, положението на равновесие на системата (4) е асимптотично стабилен, ако си състояние вектор отговаря на условията (11).
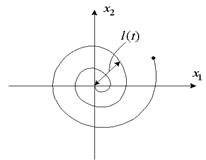
Ако позицията на равновесие на системата е асимптотично стабилна, разстоянието от представителна точка на произхода намалява с времето, вероятно не-монотонно като например е показано на фиг. 4. Ако системата не е неповторимо място е асимптотично стабилна, това разстояние не се намалява с.
Идеята на втория метод е да се конструира Lyapunov някои функция. в зависимост от вектора на състоянието на системата в процес на проучване, позитивен и монотонно намалява с намаляване. Ако тази функция е да отида до нула, като разстоянието на представителна точка от равновесното положение, след което ясно е подходящо равновесие позиция е асимптотично стабилна.
С други думи, стабилността или нестабилността на невъзмутим система на движение може да се настрои чрез изследване на поведението на функцията с течение на времето.
Тези функции се наричат Ляпунов функции. Lyapunov функция обикновено винаги по-голяма от нула и има отрицателно производно време (в случая на стабилността на положението на равновесие), определена на траекториите на системата по проучване.
В тази връзка, ние смятаме, концепцията на определена функция, т. Е. Положителна (отрицателна) определен и постоянен знак е положителен (отрицателно) semidefinite функции, както и понятието производно по отношение на времето по траекториите на динамична система.
Помислете за функцията. Нека тази функция е диференцируема, т.е. негови частични производни съществуват изобщо.
Определение. Функцията се нарича положителен, ако за всяко определено
Положителен определена функция е показана. Положителни определени функции с са, например, функция
Определение. Функцията се нарича положителен semidefinite ако
Положителен полу-определена функция е посочено. Положителен полу-определена функция с, например, функцията
Отрицателно дефинирана функция се определя, както следва:
посочено Отрицателна определена функция. и отрицателни semidefinite.
Определение. Функцията се нарича безкрайна, ако за всяко число има, които са извън обхвата на неравенството.
Квадратните форми. Често като определена функция използване квадратичен форми, т.е.. Е. вида на функция
Матрицата Р квадратичен форми обикновено са симетрични матрици, т.е.. Е. тези, в които
Условия за положителни определени квадратни форми с симетрична матрица са, както следва.
критерий Силвестър. За положителен определеност на квадратна форма (13), (14), е необходимо и достатъчно всички диагонални непълнолетни на матрица Р са строго по-голямо от нула.
Matrix P отговаря на критерия за Силвестър, наречена положителен определен и също така се нарича.
Нека P матрица е симетрична, т.е.. Д.
За да прогнозирате знак, категоричността на матрицата намираме от следните квалификации:
След това, в съответствие с критерия за Силвестър матрица. ако
Определяне на производната по отношение на времето по траекториите на системата. Това производно играе важна роля в изследвания на стабилността на движението на динамичната система от функцията Lyapunov. Помислете функция. относно определени система променливи на състоянието (4). Ние считаме, неговите производни, по отношение на времето по траекториите на системата. Като общо правило за диференциране композитни функции
Въпреки това, с оглед на уравнение (4). Следователно, производно време на функция V (х) по протежение на траекторията на системата (4) се дава от
Пример 2. Да. и уравненията на системата са на формуляра. Намерете производната на функция от времето заедно траекториите на дадената система.
Решение. Според формули (16) и (17) намираме
или с определени уравнения и:
Както може да се види, производното е отрицателен определен. Това показва, че функцията е монотонно успокояван, намаляваща величина в. Тъй като само може да намали с намаляване. нормата на разтвора на системата, очевидно клони към нула. И това се отнася и за всички начални условия. Следователно, позицията на равновесие на системата е асимптотично стабилна като цяло.
Имайте предвид, че този извод е без решаване на диференциални уравнения, дадени нелинейна система, както и всякакви други математически операции върху тях.
В основата на втория метод Lyapunov за изследване на динамични движения системи включват следните теорема [2, 20].
Теорема 4 (асимптотичната стабилност). Ако символът
всички има положително определена функция, така че нейната производна по отношение на времето по траекториите на системата (4) е отрицателна определена функция, тогава състоянието на равновесие на системата е асимптотично стабилен в голям.
Теорема 5 (нестабилност). Ако изобщо. има положително определена функция, така че нейната производна по отношение на времето по траекториите на системата (2) също е положително определена функция, положението на равновесие на системата е нестабилна.
Теорема 6 (Барбашин-Krasousky). Ако изобщо има безкрайно голяма принудително определена функция, така че нейната производна по отношение на времето по траекториите на системата (4) е отрицателен полу-определена функция, но изчезва на набор, който не съдържа цели траектории (с изключение на положението на равновесие) на системата (4) позицията равновесие на системата (4) е асимптотично стабилна като цяло.
Положителни-определена функция. отговаря теорема върху стабилността или нестабилност във връзка със система, наречена функция Lyapunov на системата. Имайте предвид също, че ако функцията Ляпунов отговаря на определена стабилност теорема не навсякъде в пространството, но само в определена област, включително положението на равновесие, този регион е регион на привличане на съответния равновесие позиция.
Ето някои примери за изследване на стабилността на движение на нелинейни системи чрез метода на Ляпунов функции.
Свързани статии
