Определяне на функцията на Ляпунов
функция Lyapunov е скаларна функция на фаза пространство на система, която може да се използва да се докаже стабилността на положението на равновесие. метод Lyapunov функция се използва за изследване на стабилността на различните диференциални уравнения и системи. По-долу ние се ограничаваме до автономните системи \ [= \ mathbf \ ляво (\ mathbf \ вдясно) \; \; \ текст> \; \; >>> = \ наляво (,, \ ldots,> \ вдясно),> \; \; \] С позиция нула равновесие \ (\ mathbf \ екв \ mathbf. \)
Да предположим, че в определен квартал \ (U \) произход даден непрекъснато диференцируема функция \ [V \ ляв (,, \ ldots,> \ вдясно) V \ ляв (\ mathbf \ вдясно) =. \] Да \ (V \ ляв (\ mathbf \ дясно)> 0 \) за всички \ (\ mathbf \ в U \ наклонена черта \ лява \<\mathbf \right\>,\), И по произход \ на (V \ наляво (\ mathbf \ дясно) = 0. \) Тези функции са, например, функции на форма \ [,> \ дясно) = ax_1 ^ 2 + bx_2 ^ 2> \; \ ; ,> \ Десен) = ax_1 ^ 2 + bx_2 ^ 4> \; \; 0.> \] Сега намерите общо производно функция \ (V \ ляво (\ mathbf \ дясно) \) Време \ (т: \) \ [>> = \ Frac >>> \ Frac >>> + \ Frac >> > \ Frac >>> + \ cdots> + >>> \ Frac >>>> \] Тази експресия могат да бъдат написани като скаларен продукт на два вектора :. \ [>> = \ наляво (\, V \ Frac >> >> \ вдясно), \; \; \ текст \; \; >>>> \ Фрак >>> \ ldots \ Фрак >>>> \ вдясно),> \; \; >>> = \ наляво (>>> \ Frac >>> \ ldots \ Frac >>>> \ дясно).> \] Тук, първият вектор е функция градиент \ (V \ наляво (\ mathbf \ полето), \) т например гости-. винаги е насочена в посока на максимално увеличение на функция \ (V \ наляво (\ mathbf \ дясно). \) Обикновено функция \ (V \ наляво (\ mathbf \ дясно) \) се увеличава с разстоянието от произхода, т.е. под условие \ (. \ лява | \ mathbf \ дясна | \ да \ infty \) Вторият елемент на скаларна продукт - е вектор на скоростта. Във всеки момент тя е насочена към една допирателна към траекторията на фаза.
Да разгледаме случая, когато производното \ на (V \ ляв (\ mathbf \ вдясно) \) в квартал \ (U \) произходът е отрицателен: \ [\ Фрак >> = \ ляво (\, V, \ Фрак >>>> \ вдясно) 0 \) за всички \ (\ mathbf \ в U \ наклонена черта \ лява \<\mathbf \right\>\);
\ (V \ наляво (\ mathbf \ полето) = 0 \);
стабилност теореми
Теорема на стабилността в смисъл на Ляпунов. Ако съседство \ (U \) нулеви разтвори \ (\ mathbf = \ mathbf \) автономна система съществува Lyapunov функция \ (V \ наляво (\ mathbf \ полето), \) равновесно положение \ на (\ mathbf = \ mathbf \ ) е Lyapunov стабилна.
На теоремата на асимптотичната стабилност. Ако съседство \ (U \) решения нула \ (\ mathbf = \ mathbf \) е автономна система на Lyapunov функция \ (V \ наляво (\ mathbf \ дясно) \) с отрицателен определено производно \ (>> \ normalsize> 0 \).
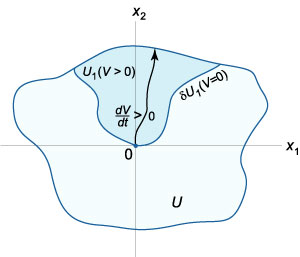
Ако квартал \ (U \) има точки, в които \ (V \ ляво (\ mathbf \ дясно)> 0, \), а след това на хомогенен разтвор \ (\ mathbf = \ mathbf \) е нестабилен. Теорема Chetaev на нестабилност. Да предположим, че в квартал \ (U \) нулеви решения \ (\ mathbf = \ mathbf \) автономна система, налице е непрекъснато диференцируема функция \ (V \ ляв (\ mathbf \ вдясно). \) Нека квартал \ (U \) съдържа поддомейн \ ( \), включително произход (фиг. \ (3 \)), така че
\ (V \ ляв (\ mathbf \ дясно)> 0 \) за всички \ (\ mathbf \ в \ наклонена черта \ ляво \<\mathbf \right\>\);
\ (V \ наляво (\ mathbf \ полето) = 0 \) за всички \ (\ mathbf \ в \ делта, \), където \ (\ б \) представлява границата подучастъци \ (\).
Тогава нула решение \ (\ mathbf = \ mathbf \) системата е нестабилна. В този случай траекториите фаза в поддомейн \ (\) ще потърсят от произхода.
Така, функцията Liapunov позволява да се установи стабилността или нестабилност на системата. Предимството на този метод е, че не е необходимо да се знае, самото решение \ (\ mathbf \ ляв (т \ вдясно) \.) Освен това, този метод ни позволява да разследва стабилността на равновесните позиции на нестабилни системи - например, в случаите, когато точката на равновесие е център. Недостатъкът е, че не съществува общ метод за конструиране Ляпунов функции. В конкретния случай на хомогенни автономни системи с постоянни коефициенти на функция Lyapunov може да се намери под формата на квадратна форма.
Свързани статии
