координатна трансформация матрица
Потопете се в пространството е н и две различни база е 1, д 2. д н и E 1, E 2. Е н
Разсъждение ще се проведе за случая, п = 3. Един и същи вектор х по отношение на различни бази имат различни координати. Можем да напишем:
Всеки вектор на втората база може да се разшири в първата основа, т.е.
Чрез уникалността на разлагането на основата трябва да се равнява на коефициентите на вектори Е1, Е2, Е3 и получени. след това
Представяме предвид матрицата
След това тези отношения могат да бъдат написани в матрична форма, X = Z ⋅ Х ".
Z матрица се нарича матрицата на координатна трансформация при прехода от старата към нова основа, т.е. от изходното ниво е 1, е 2. д п към базовата Е 1, Е 2. Е п. Освен това, координатна трансформация матрични колони са координатите на нова основа вектори е 1, Е пЕ 2. относително стари база е 1, п е 2. напр.
Промяна на матрицата на линеен оператор в прехода към нова база
Нека E п в пространството определено линеен оператор А. т.е. у = А ⋅ х
Или Y = A⋅X. където X (X 1, X 2 х п) и Т Y (у 1, у 2. у п) T матрични колони, с представяне на координатите на вектори X и Y по отношение на база п от 1, 2. д е н. А - матрица на линеен оператор А.
Изберете в същото пространство като друга основа Е н E 1, E 2. Е н. Сравнително нова основа матрица на линеен оператор ще бъде различен. Означаваме Т матрица на преобразуването на координати, и X 'и Y' - една колона матрица, съставена от координатите на векторите на х и у, по отношение на нова основа, т.е.
Заместването на тази в изглед в перспектива, след това ние получаваме: Т ⋅ Y '= A T ⋅ ⋅ X'
Увеличаването на лявата и дясната страна на уравнение в ляво от Т -1. ние получаваме: Y '= T -1 ⋅ ⋅ A T ⋅ X'.
Така че, ако Е н отидете на нова основа, матрицата на линейния оператор също ще се промени, а в общия случай ще бъде равна на T -1 ⋅ ⋅ А Т.
Пример. Оператор в основата на пространство E 3
Намери своята матрица, в основата
Решение: Matrix оператор в нова основа от формула В = T -1 АТ. където Т - матрица на преход от стария към новия основа. Трансформация матрица от формула Т = X -1 ⋅ Y.
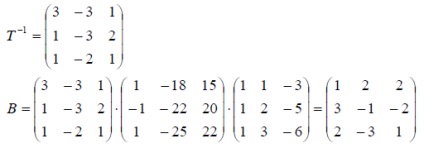
Долепени и самостоятелно долепени оператор
Да предположим, че в реалния евклидово пространство E п се определя линеен оператор
Определение 1. Оператор A * в реално евклидово пространство E п се нарича конюгат по отношение на линейната оператор в едно и също пространство, ако матрицата във всеки ортонормирана база на пространството е nirovannoy транспонирана матрица по отношение на оператор А.
Свойствата на оператора на долепени
1. E * = E, където Е - операторът на идентичност, т.е. оператор, матрицата, в която Е единица E п
4. Ако -1 съществува, тогава (А-1) * = (А *) -1.
Определение 2. А. линеен оператор е определена в истинско евклидово пространство E п. Той нарича себе си долепени. или симетричен. ако той дава covpa с прилежаща оператор A *. т.е. ако А * = А.
долепени оператор съвпада с транспонирана матрица във всяка база ортонормирана, т.е. Тя е симетрична спрямо главния диагонал.
Свойствата на самостоятелно долепени оператор
1. ако A * = A. B * = B. след това (А + В) * = A * + B * = А + В;
2. Ако А - nondegenerate долепени оператор, след това (А-1) * = (А *) -1 = A -1.
Доказателство. Всъщност, ако А -1 съществува и в допълнение A * = А. след това от свойства на оператора на конюгат 4, ние получаваме (А-1) * = (А *) -1 = А 1;
3. Ако A - долепени оператор в реалното пространство е н. следното уравнение притежава:
Собствени вектори и собствени стойности на линеен оператор
Нека A - линеен оператор. Нека x∈Ε 1. 1, където Ε на подпространство на E п. у = А вектор х може да принадлежи подпространство Ε 1. или не могат да принадлежат към лежат.
Определение. Подпространството Ε 1 се нарича инвариант спрямо koperatoruA. ако А x∈ Ε 1. ∀x∈ Ε 1.
Определение. Ненулеви вектор х се нарича собствен вектор на линеен оператор А. Ако съществува брой λ. това е равенство А х = λ х. Освен това, ламбда номер се нарича собствена стойност (собствен номер) operatoraA. съответстваща на вектор х. Множеството от всички собствени стойности на А се нарича спектър.
Нека се спрем на намиране на собствени стойности и собствени на линеен оператор А. Разглеждане на разходите за случая с п 3. Така че, нека по някакъв основа на оператор има матрица
и нека вертикалната масива съответства на вектор х. По дефиниция
Въпросът е намалена до решаване на система за линейни уравнения хомогенни написани в матрична форма. Очевидно е, че тази система има nontrivial разтвор ако Det (А - λE) = 0. Det на уравнение (А - λE) = 0 е характеристика уравнението на оператор А; полином Det (А - λE) нарича съответно mnogochlenomoperatoraA характеристика. В координатна образуват характерната уравнението изглежда така:
Вземането на решение то, ние откриваме - собствените стойности на оператора на линейна. Освен това, за сумата на диагоналните елементи на матрицата А. наречен тази матрица TRA следа или следа оператор А (TRA). следната формула притежава. Освен това, DETA = λ 1 λ 2 λ 3.
След като намери собствените стойности на линеен оператор А. остава да ги заместят един по един в уравнението и да намерят съответните собствени вектори X (1). х (2). х (3)
Пример. Намери собствените стойности и собствените стойности на оператора на линеен чиято матрица
Решение. По дефиниция, ние можем да напишете свой собствен вектор - матрица - колона Съответният неизвестен вектор х на линеен оператор А;
В матрична форма получаваме:
хомогенна система, поради това, че има безкраен брой решения, ако детерминанта е нула, т.е. Имаме характеристика уравнение:
Решаването на това уравнение, ние получаваме такива собствени стойности Л 1 = 1; λ 2 = 3.
Ние намираме съответните собствени вектори.
1) λ 1 = -1 заместител в уравнението, получаваме
където т (1) - параметър. По този начин, ние имаме множество колинеарни вектори, съответстващи на първата собствена стойност ДълЖината 1 = 1:
Този вектор не е трудно да се нормализира, след това се единица собствен вектор, съответстващ на първата собствена стойност ДълЖината 1 = -1 т.е.
2) Х2 = 3 заместител уравнението, получаваме
Накрая се отбележи, че множеството на всички вектори у = А х. където x∈ E п. Тя се нарича областта на оператор линейна ценности E п. и множеството на всички вектори x∈Ε 1 ⊂ E п. така че А х = 0, се нарича ядрото на линеен оператор.
Свойствата на собствени стойности и собствени на оператор на самостоятелно долепени
Помислете за себе си долепени оператор А. определен в реалния евклидово пространство E н. Чрез определянето на симетрична матрица го.
Теорема 1. Собствените стойности на самостоятелно долепени оператор А е реално число.
Теорема 2. Собствени вектори, съответстващи на два различни собствени стойности на самостоятелно долепени оператор са взаимно перпендикулярни.
> Доказателство. Да - различни собствени стойности на самостоятелно долепени оператор А. и х 1. х 2 - съответните собствени стойности. след това
Но това е Лявата страни са равни, като по този начин се извади техния срок от термин, получаваме, и това означава, че собствените вектори х 1. х 2 ортогонална.
Забележка. Тъй като собствени вектори са ортогонални самостоятелно долепени оператор А, може да се приема като основа за вектор пространството, в което е определено линейно оператора. По-нататък се раздели всеки вектор с дължината си, ние получаваме ortonor рана основа.
Теорема 3. В основата на единичните собствени вектори на оператор самостоятелно долепени на матрицата на оператор диагонал с диагонални елементи са неговите собствени стойности.
Доказателство. Доказателството е по за случая N = 3. Да е 1. 2. д д 3 - единичен вектор на самостоятелно долепени оператор по отношение на базата на линейния пространство E 3. съответстваща на собствените стойности на оператора на линеен, т.е. , Да приемем вектори д 1. д 2. д 3 за основа на линеен пространство. Очевидно е, че в тази база вектори имат координати:
. Следователно матрица А в база отчета за А е 1. 2. д д 3 има формата:
Изборът на такава база, при което матрицата на линеен оператор е диагонална, тя се нарича понижено матрицата да диагонал форма.
Свързани статии
