Теорема 2. равнина, която не е преминала през най-високата точка на прав кръгов конус, като преминава в елипса, ако тя пресича всички генератори на конуса (вж. Ris.190), парабола, ако тя е успоредна на само един на конуса (вж. Ris.191) и хипербола ако е успоредна на две образуващите на конуса (Вж. ris.192).
Доказателство. За да докаже това, помислете прав кръгов конус, който в правоъгълна координатна система се описва с уравнението:
и геометрично получен чрез въртене около оста на линията. собственост координира SVOCs-кост. Чрез кръгова повърхност на симетрия (6) може да се ограничи само до секциите на Pomeau-супа равнини, перпендикулярни координира-ASW равнина. В тази равнина съответства на уравнението. ,
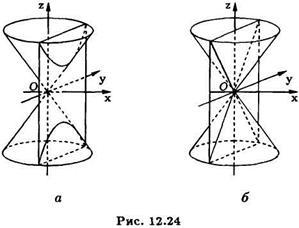
Ако. рязане равнина, описана от уравнението. където паралела координатната равнина. Заместването на стойността на абсцисата на конуса в уравнение (6), ние откриваме, че напречното сечение в равнина, описана от уравнението и определя равностранен хипербола (Вж. Ris.12.24), а двойка линии, които са образуващите на конуса. Ris.12.24.
Сега предполагам, че в уравнението на коефициента на пресичащи се самолет. След това самолетът може да бъде представляван от уравнението. къде. , Поради симетрията на конус спрямо равнината достатъчно да разгледаме случая, когато.
Коничната секция за дадена равнина в пространството е описано чрез система от две уравнения (7)
За да се получи уравнението на пресичаща равнината, помислете за правоъгълна координатна система,
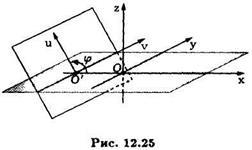
вземайки като координатните оси и линиите, които са на пресичане на равнината на рязане с координатната равнини и (виж фиг. 12,25).
И координати на произволна точка в равнината на рязане ще бъдат свързани с неговите координати. и в пространството на отношенията:
където - ъгълът между коничната секция перпендикулярна на референтната равнина. и координатната равнина. и. а.
Заместването (8) в първото уравнение на (7), т.е. в уравнението. получаваме уравнение на конично сечение в координатна система:
. Скобите и други подобни термини, които намираме:
Когато. когато рязане равнина образува равнина със същия ъгъл като конус образуване на коничната секция ще бъде парабола (виж фиг ..), и е описано от уравнението:
Чрез промяна на параметъра в Уравнение рязане равнина като конична секция може да се получи всяка парабола.
Когато. Уравнение (9) е:
Има две възможности. Когато. т.е. когато сечащ равнина образуващ с по-малък ъгъл от конуса образуване неравенството и, следователно, уравнението (10) е конично сечение уравнение на елипсата (Вж. Фиг. 12.26) ще бъдат удовлетворени.
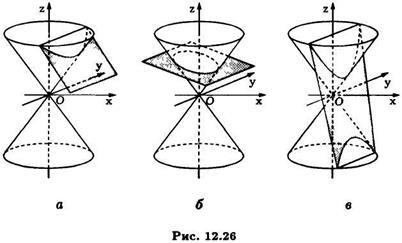
Тук различна параметрите в уравнението на пресичаща равнината, ние можем да получите във всеки раздел елипса.
Когато. т.е. когато рязане равнина образува плоскост с по-голям ъгъл от производителите на конус, ние имаме. така че конусният участък е описано от уравнението (10) ще бъде хипербола (Вж. Фиг.). Чрез вариране на параметрите и могат да бъдат получени във всеки конично сечение хипербола.
