Определение 7. Ако (8.1) е възможно само ако всички а1 вектори. А2. aknazyvayutsyalineyno независими.
Определение 8. Ако равенство притежава, тогава ние казваме, че вектор б yavlyaetsyalineynoy комбинация от вектори a1 на. А2. ак. ililineynovyrazhaetsya чрез тези вектори.
Имайте предвид, че ако а1 вектори. А2. ак са линейно зависими, тогава поне един от векторите може да бъде линейно изразена по отношение на другия. Това следва от определението за 6, като че ли най-малко един от, тогава е възможно да се извърши до края на разделението, и тогава ние ще бъдем там, където. Обратното е вярно, че ако един от векторите е линейно изразена чрез останалите, всички тези вектори заедно са линейно зависими.
Имайте предвид, че ако вектори А и В не лежат на една права или. б и в не лежат в една равнина. След това тези вектори са линейно независими, съответно в равнината или в пространството.
Ние показваме в този пример, три не-копланарни векторите на. б и в. Доказателство от противоречие, предполагайки, че тези вектори но не копланарни. но линейно зависими. След това той трябва да отговаря на условието за линейна зависимост на вектори, т.е. и може в същото време. След това, можете да се разделят на лявата и дясната страна на уравнението и резултатът ще бъде израз което противоречи на определението за 10 ( ""), т.е. Въпреки векторите на. б и в не лежат в една равнина. но вектора линейна комбинация от другите два б и в. който казва (както е определено в 8) на линеен връзката им. От това следва, че вектор трябва да бъде линейно независими вектори на б и в. Интересното е, че в триизмерното пространство, всички четири пространствени вектори са линейно зависими.
Две ненулеви вектори а и б са ортогонални. ако те са перпендикулярни (проекцията на вектор, б, и проекцията на вектора б до нула). След това напишете. Такива вектори са винаги линейно независими.
Ако не е нула векторите на. В и С са по двойки ортогонална, тогава те формират три линейно независими вектори.
Определение 9. Rangomsistemy вектори е максималният брой на линейно независими вектори.
Определяне 10. линеен пространство се нарича п двумерен. ако може да се намери п линейно независими вектори, и всяка система, състояща се от по-голям брой вектори е линейно зависим от това пространство.
Така например, вектори, които лежат на една права линия. образуват един тримерно пространство. в които само един независим вектор. и всичко останало може да се изрази чрез линейни уравнения чрез него. В самолета множество вектори образува двумерен пространство. т.е. в това пространство са определени само две независими вектори.
Определение 11. Ако пространството е с ограничен набор от линейно независими вектори, а след това nazyvayutkonechnomernym. и ако може да се намери на произволен брой линейно независими вектори е - безкрайно.
Определяне 12. Наборът от п линейно независими единичен вектор в п-тримерно пространство nazyvayutbazisom п тримерно пространство.
Имайте предвид, че в основата вектори чрез всякакви други вектори, определени в тази основа може да се изрази.
Теорема. Всеки вектор х линеен п тримерно пространство може да бъде представен еднозначно под формата на линейна комбинация на базисни вектори.
Доказателство състои от две части. Започваме с възможност да изразят произволна вектор на базата на линейния пространство. а след това, че разлагането на произволен вектор на базата само.
Да предположим произволна основа п R тримерно пространство и произволно вектор. Тъй като всеки N + 1 вектори са линейно независими п R тримерно пространство (Определение 6), системата, която образува L1 вектори. L2. LN и х трябва да бъде линейно зависими. Това означава, че равенството
където - броя на едновременно не са нула. Ясно е, че, тъй като в противен случай най-малко едно от числата не ще бъде нула и по този начин уравнение (8.2) ще има формата
това на свой ред. То ще демонстрира линейна зависимост на базисни вектори. Ние изрази X в уравнение (8.2), разделяне на коефициентите на Li и преместването им в дясната страна. След извършване на тези трансформации са
Ние сега се докаже, че разширяването (8.4) на вектор х, въз основа, L1. L2. Въ само. Да приемем, че вектор х в пространство R има две различни разширения
След това се изважда една от друга между половете, а от лявата страна е един и същ вектор. Взимаме
Ето защо, ние имаме система
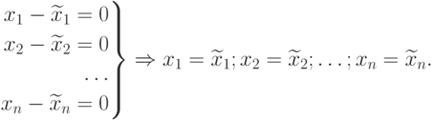
Последният израз е напълно доказва теорема.
Свързани статии
