Кратко описание на документа:
Следващият пример разглежда прилагането на концепцията за производно на решението на геометрични проблеми. За да направите това, първо разкрива концепцията за допирателна. На координатната равнина е представена от функция графика маркирани две точки М и S. през линия маркирани точка се извършва. Тя показва как в S точка приближаването точка М на правата линия, свързваща позиция подходи позицията на допирателната в точката М. Това е допирателна представлява крайно положение на пресичане чрез две точки, генерирани по време на точките на подхода. След въвеждане на понятието допирателна счита допирателна към графиката на у = е (х) в точка М (а, е (а)). Необходимо е да се намери коефициент ъгъла тангента. За тази цел, на известно разстояние от точката маркиран М Н (А + ьН, е (а + ьН)). Наклон на линията е допирателна на ъгъла, под който се намира линията съдържащ хипотенузата на триъгълник, образуван от нарастване на аргумента и ьН δu функцията увеличение. Съответно, коефициентът на ъгъл на рязане се дава от ksek. = Δu / ьН. При приближаване точка бн → 0. Очевидно е, че по време на подхода на точките допирателни определени крайно положение сечащ при АН → 0 kkas. = Лим ksek. или kkas. = Лим δu / ьН.
Заключения от характеристиките на математически модел за решаване на двата проблема, документирани в определението за форма на функция производно, констатация, която се появява в проблеми. Трябва да се отбележи, че за функция у = е (х), дефинирани в точка х и съседните, граничната δu / ьН в ьН → 0 е производно на у = е (х) в тази точка. Представяме означението на производно F '(X). За абсорбция материал се счита производно на линейна функция - да се отбележи, че тъй като е установено, преди това за функция Y = KX + m граница Lim δu / ьН в бн = к → 0, Y '= (KX + m)' = к. Също така, установено граница функция у = х 3. равно Lim δu / бн = 3x 2 в ьН 0 → означава, че у производно '= (х 3) = 3 2.
Това показва физическата и геометрична смисъла на производно. Трябва да се отбележи, че във физическия смисъл закона за праволинейно движение и (т) е производно на моментната скорост V = S "(Т). В геометричния смисъл на допирателна. провежда при х = а на графиката на у = е (х) на производно F '(а) - наклона на допирателната.
Като се има предвид значението на производно и формула за намиране Lim δu / бн = F '(х) при ьН → 0, има почти право пропорционална функция нарастване на нарастване на аргумента с коефициент, представляващ производно δu≈f' (х) · ьН. Така, производното на функция у = х 3 δu≈3h вярно съотношение 2 · ьН.
Алгоритъм функцията производно, което е необходимо:
- В търсене на точка х F на (х);
- В прехода към точката х + ьН намери е (х + бн);
- Виж нарастването на F функция (х + ьН) - е (х);
- Създаване съотношение δu / ьН;
- Виж Lim δu / ьН в ьН → 0, т.е. F '(х).
Според този алгоритъм са показани примери за откриване на производно функция F на (х) = С, където (С) = 0; е (х) = 1 / х, където (1 / х) = - 1 / х 2.
Идеята за диференциация на функциите, тоест, да намерите неговите производни. Отбелязва се, че функцията е диференцируема в точката, ако има в него производно и диференцируема функция в точка е непрекъснатостта на него, и обратното не е вярно. Потвърждаване на одобрение на този пример е да се намери производно в точка х = 0 на у функция = | х |. Следва да се отбележи, че независимо от непрекъснатостта на функцията в този момент, допирателната към графика не може да има. А това означава, и там е в този момент на деривата. Това заключение се показва на екрана отделно и се препоръчва за съхранение. Един пример на приемане е функция у = F (X), в която X<0 равна -√-х, а на промежутке x>= 0 е равна на √h. фигура изобразени функционира, когато е непрекъснатостта на добре видими. Въпреки това, при х = 0, допирателна към графиката не може да бъде изградена, така че в този момент не е производно. Припомни, че ако в някакъв момент от графиката на допирателната не може да бъде изграден, или е перпендикулярна на оста х, без диференцируема функция. В този пример, диференцируема функция. На произволна графика на пример за последното се счита диференцируемост в три точки.

Помислете два различни задачи, физични и геометрични, които и двете водят до появата на нов математически модел.
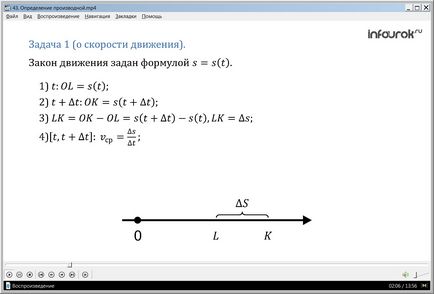
Задача 1 (скоростта на превозното средство). Според линията, на която са изложени на контролната точка, устройството (м) и посоката, движещо се тяло (материална точка) а. Законът за движение, определен от формула S = S (Т) (ES равни ES ТЕ), където Т - време (секунди), S (у) - позиция на тялото на правата линия (координират движи материал точка) в момент по отношение на върха препратка (в метри). Виж скорост на тялото по време на тон (в м / сек).
Решение. Да предположим, че по време на т е в точката на тялото
L (фиг. 1), нараства от началото на движение OL = S (т). Нека да даде аргумент тон
нарастване DT (делта ТЕ) и разгледа време Т + АТ. Координатна материал точка става друг орган в този момент е в точка К: ОК = S (T + T) (равни на около ка ES ТЕ ТЕ плюс делта).
Така че, за Т секунди тяло се премества от точка до точка L К, т.е. ЛК приет начин. Ние имаме: LK = OK-ол = S (T + T) -S (т). Получената разликата ние име увеличение функция: и (т + т) -S (у) = S. Така че, LK = (M).
Path и (м) телесна държани за тон секунди. Това е лесно да се намери средната скорост на движение по време на интервала от време [т, т + т]: VAV. = (М / с) (средната скорост е равна на относителната делта ES ТЕ делта).
Какво е скорост V (т) по време на тон (понякога се нарича си моментната скорост). Може да се каже, че това е средната скорост по време на интервал от време [т, т + т] при условие, че т е по-малко и по-малко е избран; с други думи, при условие, че T0. Това означава, че
о (т) = (Ve от ТЕ граница равна на средната скорост) и
Обобщавайки решаване на проблема 1, получаваме:
За да се реши следния проблем, ние трябва да разберем какво се разбира под допирателната към кривата.
(. Фигура 2) Dana крива L него избрана точка М. Ние приемаме друга точка на кривата, и достатъчно близо до М, - точката С.
Направи преминаване MS. След това ще се увеличи точка S на крива L до
точка М. метат MS ще промени своята позиция, изглежда да се върти около точката М. Това често се случва, че може да се намери в линията на процес, който е определен ограничаване позиция на пресичане; това право - най-добрата позиция на разреза - нарича
L допирателна към кривата в точка М.
Задача 2 (о допирателна към графиката). Dan графика на у = е (х). Той избрана точка M (а; е (а)) (хм координира и Aeff на а). в този момент на графиката на допирателните (ние се предположи, че съществува).
Намери склона тангента.
Решение. Даваме аргумент увеличение х и помисли графиката (фиг. 3), точката с абсциса N A + х. Ординатата на точка п е равно на е (а + х). Наклонът на пресичащия MN. т.е. ъгълът между допирателната и сечащ ос х. Тя се изчислява по формулата (к е равно на пресичане делта у разделена на делта X).
Ако сега ние нека х до нула, точка N на кривата започва да се доближава до точка М. тангента ние характеризира
като ограничаване на позицията на пресичане с това сближаване. Следователно, разбира се предположи, че съотношението на ъгъл допирателна kkac се изчислява по формулата (ка ка допирателна равно граница сечащ).
Като се използва формулата за ksek горе. получаване (ка допирателна равно граница делта у разделена на делта X, X делта клони към нула).
За да обобщим. В процеса на решаване на двата проблема, ние стигнахме до едно и също математически модел - на граничната съотношението на функцията за увеличение на нарастване на аргумента, където нарастването на аргумента клони към нула.
Помислете за това, което ограничение от съотношението на функцията за увеличение на нарастване на аргумента.
2. Определяне на производно
Определение 1. Нека функция у = F (х) се определя в определен момент х в даден район. Ние даваме на аргумента х нарастване на х, така че да не оставят този квартал. Ние намираме съответните функции на прираста δu и съотношението състав. Ако граница на това съотношение е предвидено x0, това ограничение се нарича производно с функция у = F (х) на х и означен F '(х) (EFF бар на X).
По този начин, (границата на делта у разделена на делта Х означава EF бар на X).
За да се определи производно често се използва в герой ". (Y бар)
Отбелязваме, че Y '= F' (х) (у бар е EF бар на X) - е нова функция, но свързан с функция у = F (х), дефинирано във всички тези точки X, в която има над границата на , Тази функция се нарича както следва: производното на функция у = F (х).
В един пример за линейна функция у = KX + m равенство.
Това означава, че Y '= к или повече,
Ние сме доказали, че у функция = х 3 равенство
Това означава, че у = 3x 2 или повече, (х 3) = 3 2. (X кубчета бар X е равно на три във втората степен)
Производно с физическите и геометрични гледни точки.
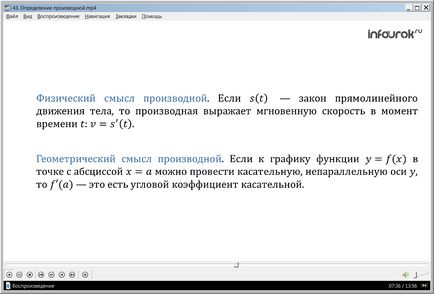
Физическа (механични) смисъл на производното е както следва. Ако е (Т) - закона на праволинейно движение на тялото, тогава производното изразява моментната скорост по време на т:
V = S '(T) (ве равно инсулт ТЕ и).
Геометрична смисъла на производното е както следва. Ако графиката на функция у = F (х) в точката с абсцисата X = А може да се допирателна не са успоредни ос Y, F '(а) има тангенциален ъглов коефициент.
Да приемем, че функция у = F (х) е производно в определен момент х (граница на съотношението на нарастване на нарастване на функцията аргумент е функцията производно).
Получаване на достатъчно малък съседство на х приблизителното уравнение притежава: (съотношение на стъпките на нарастване на функцията аргумент приблизително равна на функцията производно) или
Y е '(х) · х. (Функция увеличение приблизително равна на функцията производно умножена по нарастване на аргумента).
Увеличаване функция "почти пропорционална" на нарастване на аргумента, фактор на пропорционалност е производно стойност (в даден момент х). Например, за функция у = х 3 следните приблизителни уравнение Y 2 · х 3
Ние формулира алгоритъм за намиране на деривата.
Алгоритъм за намиране производни (функция у = е (х))
1. За да се определи стойността на х, намерите е (х).
2. Дайте увеличените аргумент X, се премести в ново място
х + х, подреждането е (х + х).
3. Виж функцията увеличение: у = е (х + х) -f (х).
4. Създаване на съотношение.
5. Изчисли граница.
Това ограничение е F '(х).
Пример 1. Виж производното на постоянна функция у = S.
Решение. Ние използваме алгоритъма за намиране на деривата.
1) х фиксирана стойност, имаме: е (х) = C
2) В точката х + х имаме: е (х + х) = С
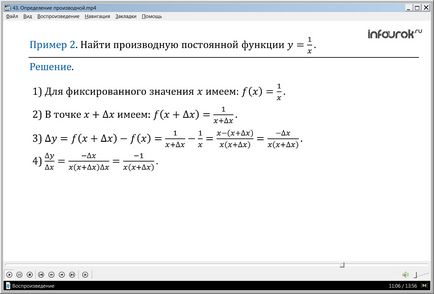
Пример 2. Виж производната на функцията = у.
Решение. Ние използваме алгоритъма за намиране на деривата.
Ако функция у = F (х) е производно в точка х, то се нарича диференцируема в точката х. Намирането на производно на функция у = F (х) се нарича получаване функция у = е (х).
Ако функцията е диференцируема в точката х, то е непрекъснат в този момент.
Обратното не е вярно.
Ето някои примери: функция у = | х | непрекъснато навсякъде и при х = 0 (Фигура 4), но допирателната към графиката на "възел точка" (0, 0) не съществува.
Ако в някакъв момент на графиката на функцията не може да се направи допирателната, след това в този момент не е производно.
Пример. Фиг. 5 показва графика на по части функция у = е (х), където
Функцията е непрекъсната по цялата реална линия, включително и в точката х = 0. И допирателната към графиката на функцията съществува навсякъде, включително в точката х = 0. Но в точката х = 0 на тангентата съвпада с у ос, т.е. перпендикулярна на абсцисата, уравнение му е форма х = 0.Takaya линия не наклон, обаче, не съществува и F '(0).
Планирана да се заключи на диференцируемост на функции, е необходимо да се провери дали е възможно в даден момент да се направи допирателна към графиката на функция, не е перпендикулярна на оста х. Ако е възможно, след това в този момент диференцируема функция. Ако в някакъв момент допирателна към графиката на функцията не съществува или е перпендикулярна на оста х, след това в този момент диференцируема функция. Така, съгласно графиката, показана на фиг. 6, можем да заключим, че функцията е непрекъсната навсякъде освен в точка х = А; функция е диференцируема навсякъде, с изключение на точки х = а и х = б - не съществува допирателна, с х = -Тук допирателна е успоредна на оста у.
