Има една важна клас на интегрални уравнения, които могат да бъдат решени лесно чрез намаляване на система от алгебрични уравнения. Тези интегрални уравнения са така наречените изродени ядките.

Определение: Ядрото на интегралната уравнение се нарича изроден, ако тя може да се представи като сума от определен брой условия, всяка от които е продукт на две функции, първият зависи само от х, а вторият - само # 958;:

Ние вярваме, че непрекъснато в [а, б], и това, както и линейно независими.

Уравнение (1) има формата:

Заместване на (29) в (1):

Тъй като. линейно независими,

Решаването на системата (32), като по този начин ще се реши този интегрално уравнение и с помощта на формула (29). Ако алгебрични система (32) не може да се реши, а след това е неразделна уравнението.

D (# 955) - полином от степен ≤ п, където D (# 955) ≠ 0, тъй # 955 = 0, D (0) = 1. Следователно, D (# 955) е ≤ N различни корени.

D (# 955) се нарича фактор Fredholm за уравнение (1).

1. Ако # 955; така, че D (# 955) ≠ 0, тогава (32), а оттам и на уравнението (1) е еднозначно определена от формула (29). В този случай, е (х) = 0, а оттам и на системата (32) има уникален разтвор; следователно # 966; (х) = 0. Това означава, че тези, # 955;, за които D (# 955) ≠ 0, а не собствените стойности.

Заключение. ако # 955; не е подходяща стойност, тогава уравнението (1) има уникален разтвор.

Очевидно е, че в нехомогенни уравнение (1) има уникален разтвор за всеки е (х) (

), Е необходимо и достатъчно съответното хомогенно уравнение има само незначителен разтвор (# 966; (х) = 0).

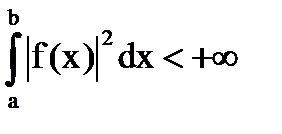
Забележка: Като общо правило, решението на интегрални уравнения често се налага да прибягват до приблизителни методи. Важно е да се установи на платежоспособността на произволно избран от дясната страна (с помощта на първата теорема). Предпочитаните е да докаже, че хомогенната уравнение, или транспонирана към него (конюгат) има само тривиално решение. Следователно, от една теорема предполага разрешимост на нехомогенни уравнение.

Три основни теорема Fredholm относно разтворимостта на уравнения с дегенерирани ядра, и може да се разшири до произволна непрекъсната сърцевина.

Намерете решението на уравнения с единични ядки:

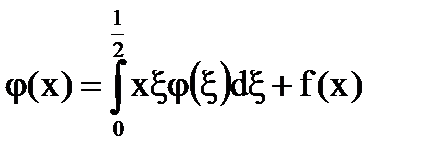
Решение: Нека

. Ние се получи. Заместник в уравнението

()

;

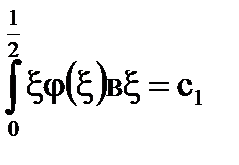
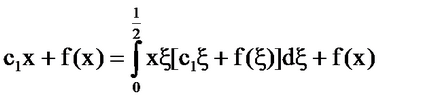
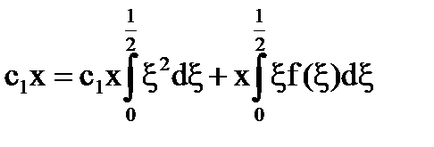
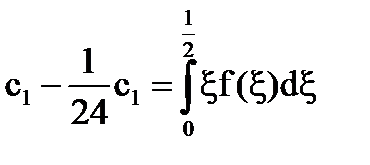
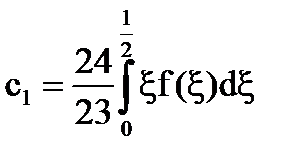
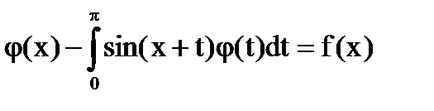
Система [5] има формата:

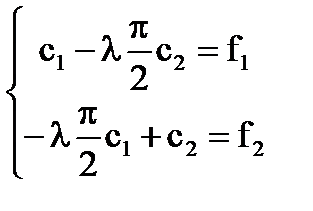
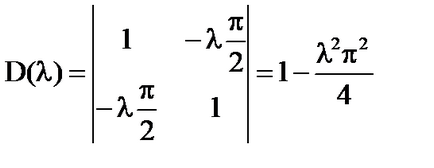
D (# 955) = 0; ; - собствените стойности на уравнението.

ако # 955; ≠. # 955; ≠. на D (# 955) ≠ 0 и системата има уникален разтвор:

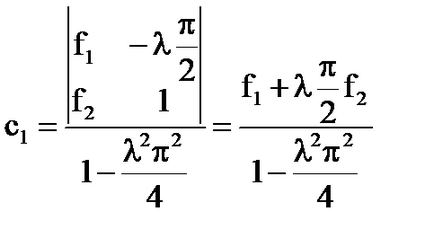
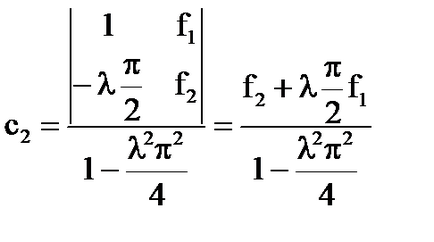
- единственото решение на уравнението неразделна

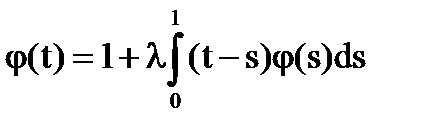
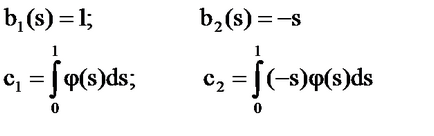
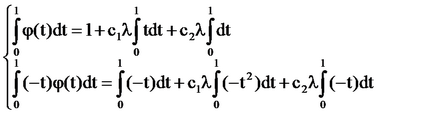
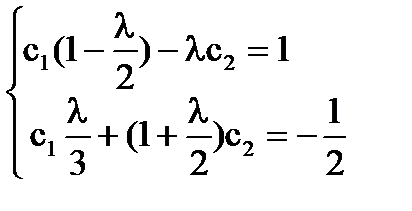
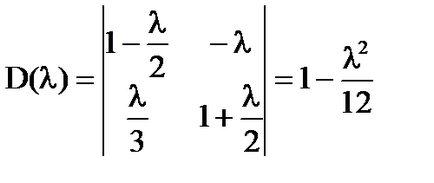
D (# 955;) ≠ 0 за всяко реално # 955;.

По правило Крамър;

Ако. единственото решение на уравнението

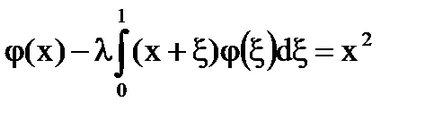
Решение: = х + # 958; - непрекъснато в кв 0 ≤ х, # 958; ≤1 и е дегенерат.

;

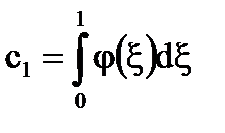
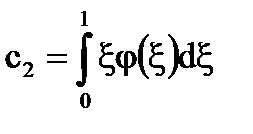
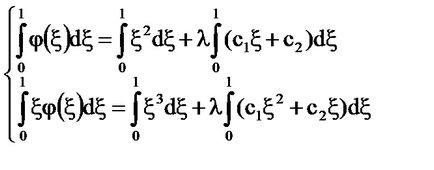
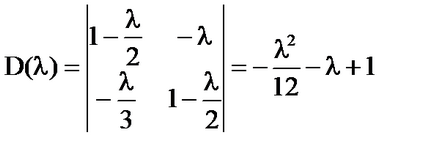
Ако. единственото решение

-

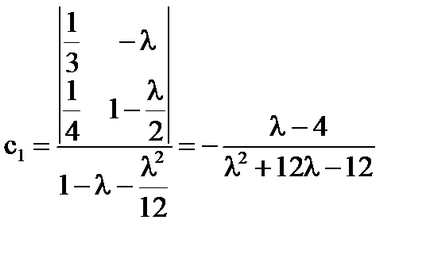
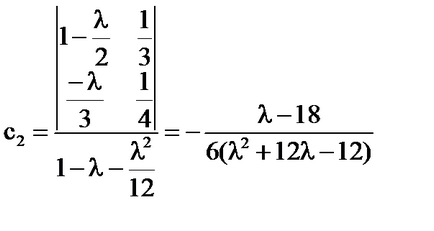
уникално решение, с.

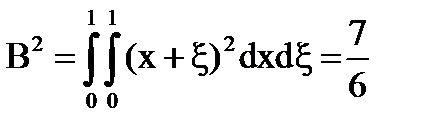
Разтвор съществува, е уникален и може да се намери чрез метода от последователни приближения в

. За останалите # 955; сближаване последователност може да се различават, въпреки че е разтвор (това е по друг начин). Тъй като условията на теоремата доказаха наличието на решения са достатъчни, но не е необходимо. За уравнения с решение дегенерат ядрото съществува и е уникален за всички # 955;, за които D (# 955) ≠ 0.

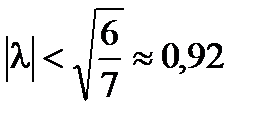
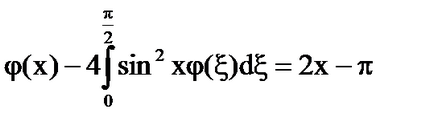
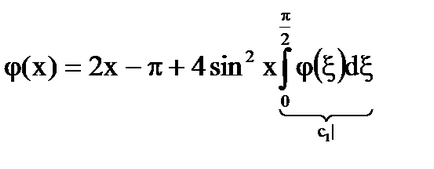
Решение: Ядро - дегенерат.

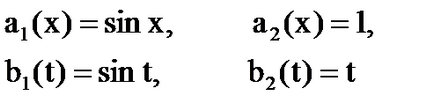
формулите [6] - [7], се изчисляват

Система [5] става

. общото му решение:

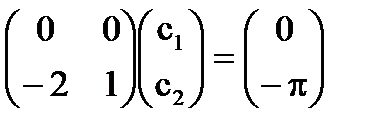
= С = -π + 2С, където С - произволна константа.

Отговор: Всяка функция на формата

е решение на уравнението неразделна и други решения на това уравнение не.

Упражнения:

Решаване на интегрални уравнения с дегенерирани ядки

Свързани статии

• Изпълнителна сила на съдебно решение - studopediya

• телеграф Двигател - studopediya

• Информация комуникация в корпоративни системи - studopediya