1. Да разгледаме областта на маса точка гравитацията е м, се поставя в о произход (0,0,0). Това поле е описан от функция вектор. където # 947; - гравитационната константа - радиус вектор на една точка. , С такова поле действа сила от теглото на единицата, се поставя в една точка. гравитационния потенциал на терена. Тя може да бъде представена като наклона на скаларна функция. наречен Нютоновата потенциал маса точка поле гравитацията м. В действителност:
2. Област на заряд е точката на електрически, се поставя в основата, точка вектор, описан в напрежение. (..) Това поле е потенциал. Тя може да бъде представена като наклона на скаларна функция. електрическо поле, което се нарича потенциала на точка такса д а ..
8. Определяне на равна повърхност (ниво линия за плоско поле) потенциал се наричат еквипотенциални повърхности (линии).
Имайте предвид, че изравняване на повърхността (линия) и вектора на линията, минаваща през една обща точка. перпендикулярни на него.
Пример 13. Тест дали поле потенциал. Ако е така, след това намерете потенциал на областта, изграждане на потенциални линии и векторно поле линия. Изберете вектор и еквипотенциални линии, преминаващи през точката.
Решение. Невярно е определен на целия самолет XOY.
Проверете дали необходимите и достатъчни условия за потенциалност изпълнени :. поле потенциал.
1. За да намерите функцията създаде система :.
От първото уравнение, като я интегрира към променливата х. намерите:
.(Ролята се играе тук като константа, всяка функция в зависимост от х). За да разберете, че се използва функцията на второто уравнение:
2.Uslovie equipotentiality. , ще получим едно семейство от еквипотенциалните линии.
Ние даваме на уравнението на каноничната форма:
Това семейство на хипербола кога.
Ако. Ние получи уравненията на линиите.
Ние изграждаме потенциални линии на самолет XOY на.
3.Vektornye линия терен. Ние формират диференциално уравнение на векторните линии на полето: .Reshim него.
- семейството на хипербола, ако. и две прави. ако. Изграждане на векторни линии на самолет XOY на.
Изравняване и векторни линии ортогонални в точки на пресичане. Проверете го за линиите, преминаващи през точката.
4.Podstavim координати на точката в уравнението векторните линии :. М преминава през точка вектор линия.
Аналогично да намерите еквипотенциална линия, минаваща през точка М. Тя преминава през точка M изравняване на линия.
Изчисляваме наклона на допирателната към тази крива в точка М:
За вектор линия: M т.:.
За еквипотенциалните линии в М R.:.
- състоянието на две перпендикулярни допирателните.
Заключение: вектор и потенциални линии на М ортогонална.
Пример 14. Уверете се, че областта е потенциален, намери потенциален поле и да се изчисли, извършена от тази област, когато се движат от материална точка работа.
Решение. За да се отговори на въпроса за потенциала на това поле се изчислява частни производни на функции. , , Тези функции са непрекъснати заедно с частични производни във всяка точка.
Ние виждаме, че следните необходими и достатъчни условия за потенциалното поле. , , , ч. т. г.
За да изчислим потенциалното използване на факта, че линията неразделна в такова поле не зависи от пътя на интеграция и може да бъде изчислена по формулата основните теорема. Нека точката - началото на пътя, но някакъв момент - края на пътя. Ние изчисли интеграл по продължение на контур, състояща се от линейни отсечки успоредни на координатните оси (виж Фигура 10). ,
Формулите на частите на верига :. , ,
. х е фиксиран, следователно,
. ето го фиксирана годишна. така.
В резултат на това ние се :.
Сега същото интеграл изчислява чрез формулата на Нютон-Лайбниц. =.
От това уравнение следва, че. и потенциала на това поле е намерен.
Ние считаме, извършена от областта на вектор, докато се придвижват от точка работа. Потенциалното областта на работа е равен на потенциалната разлика в началните и крайните точки на пътя, тоест. Д.
Пример 15. Осигуряване поле вектор потенциал. намери уравненията на еквипотенциални повърхности и избира измежду тях този, който преминава през точка М (2,1,1).
Решение. Невярно е дефинирана във всяка точка на пространството. Проверете потенциал поле (виж (11).)
условия са изпълнени, областта на потенциал. Можете да намерите потенциал по същия начин, както в пример 12, но може да бъде по друг начин. За да намерите на капацитета на системата, ние имаме:
Интегриране на първото уравнение по отношение на х на системата. намери. Разграничаваме получения израз за ш: .От второто уравнение получаваме: .Utochnim израз за потенциала:
. Диференцируема по отношение на Z и сравни с трета система уравнение :.
Възстановяване на всички функция :. Потенциалът е намерен.
Взискателни. Ние получи уравнения на еквипотенциални повърхности:
Ние даваме това уравнение за каноничната форма.
Това уравнение сфери центрирани в точка О (0, 1, 1) и радиуса
Намираме равнопотенциален повърхност, минаваща през точка М (2,1,1). Заместването координати в уравнението на повърхността, ние определяме:
Тя преминава през службите на точка M.
Намираме вектор поле линия, простираща се през точката M.
Формулите на векторни линии:
М в т: ...., т.е. преминава през т М линия. защото преминава през центъра на сферата, равнината, допирателна към сферата на т. М е перпендикулярна на нея. Е. линия вектор и еквипотенциална повърхност в т. М взаимно ортогонални.
Посоката на движение на сферата по тази линия съвпада с посоката на говедото на ос х> 0, и противоположно на това на х<0. Это совпадает с направлением увеличения потенциала U. Действительно, чем больше потенциал, тем больше радиус сферы.
Контрол задача 6.
1. Проверете дали полето за вектор е потенциал. Намери си потенциал. Изобразяват линии на равен потенциал. Намерете най-векторни линии и да ги представлява в една и съща цифра. Изчислете работа материал поле, докато се придвижват от точка до точка. Намерете най-вектор линия и еквипотенциална линия, преминаваща през точката.
2. Проверете дали потенциал поле вектор. Ако е така, намери си потенциал.
3. Намерете потенциал на гравитационното поле.
4. Покажете, че полето за вектор е потенциал и да намерят своя потенциал.
Поток векторно поле.
нека # 963; - някои ориентирана повърхност в Г. Ние избираме определена нейна страна, определянето на единица вектор нормално на повърхността.
9. Определяне на вектора на потока през повърхността # 963; Това се нарича повърхност интеграл на скаларен продукт на полето на вектора на нормалната единичен вектор: P. (13)
Има и други форми на запис вектори поток. Така например, при положение, че ние се Pr: П.
Или можете да определите вектор. насочена по нормалата към повърхността, така че :. , Тогава :. (14)
Ако повърхността # 963; затворен, обикновено за посока вектор взето перпендикулярно на посоката на външната повърхност и означават
Ако промените ориентацията (да се вземе от другата страна на повърхността), скаларната продукт и, съответно, знакът за промяна на потока.
Потокът може да бъде написана на компонент форма, представяща подходящ скаларно произведение на вектори:
където от дясната страна има повърхност интеграл от втори вид.
Всяка от условията във формула (17) се превръща в двойно неразделна над региона, който е повърхност проекция D. # 963; съответните координатна равнина:
където - проекция # 963; Oyz на координатната равнина, Oxz, Oxy съответно. Знакът пред двойна неразделна от дясната страна съвпада със знака на косинуса на ъгъла между нормалата повърхност и положителната посока на осите вол Oy, Оз, съответно. Изразите, получени чрез експресия на променливите на уравнението на повърхността # 963;:. Възможно е да се намали потока изчисление за изчисляване на интеграл от първи вид, замествайки формула (16). , ,
Пример 16. Изчисли вектор областта на потока през част от равнина. затворено в първия октант, в посока на нормална компонента на тъп ъгъл с оста OY.
С формула (13). където # 963; - равнина S :.
Припомнете си, че нормалата на уравнението на равнина има формата. В нашия проблем. Този вектор прави малък ъгъл с оста OY. След това.
Ние се намали проблема с изчисляването на интеграла I вид (вж. (13)).
Но. т.е. , От вектор алгебра е известно, че площта на триъгълник MNP (виж фигура 12) :.
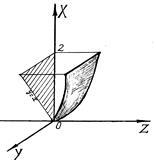
Намерете полето поток вектор през част от повърхността. ако векторът перпендикулярна на повърхността прави малък ъгъл с положителната посока на говедото на ос.
Решение. Ние образуват интеграла за изчисляване на полето на потока:
На фигура 12 се вижда, че вектора прави с ОХ остър ъгъл с OY - съответствие с OZ - тъп затова.
Изчислима. Проекцията на пресечната точка на линия и равнина YOZ :. След това: .От уравнение повърхност. след това
Изчислима. От уравнението на повърхността. след това
Резултатът може да се провери чрез намаляване на проблема с повърхност интеграл от тип I. За да направите това, да намерите и да се изчисли уюта посока. Ако повърхността на уравнението е. нормалната вектора. а.
В примера (15), уравнението на повърхността :. Като се има предвид, че нормалната вектор прави малък ъгъл с говедото на ос. Ние имаме. След това.
За да се изчисли тази неразделна аз изработи вид # 963; на XOY равнина (виж фигура 12..), след което:
От уравнението на повърхността. , ,
Контрол задача 7.
1. Виж областта на потока вектор чрез част от параболоид от двата начина, съгласно формули (15) и (17).
2. Изчислява областта на вектор поток през ориентирана повърхност # 963;, ако: а) # 963; - част от коничната повърхност. нормален външен; б) # 963; - част от равнина. ,
3. Изчислява областта на вектор поток през част от сфера.
Свързани статии
