Ние намираме собствени вектори дадени линеен оператор.
Броят е собствена стойност на оператора, ако и само ако. Пишем характерното уравнение:
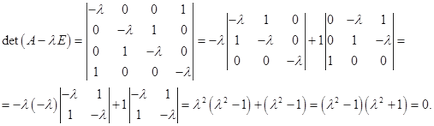
Решаването това, ние имаме
Така получаваме собствените стойности:
За всеки един от получените собствените стойности намери собствени вектори.
Те могат да намерят своите системи.
Ние решаване на хомогенна система от уравнения.
Матрицата на коефициент има ранг 2. Ние избираме като основа непълнолетния Тогава, ако приемем, ние имаме
По този начин, общото решение на системата
.
От общия брой решения намираме фундаментална система от решения:
.
Използване на основните разтвори на системата, общ разтвор може да бъде в писмена форма.
Ние решаване на хомогенна система от уравнения
.
Матрицата на коефициент има ранг 2. Ние избираме като основа непълнолетния Тогава, ако приемем, ние имаме
По този начин, общото решение на системата.
От общия брой решения намираме фундаментална система от решения:
.
Използване на основните решения на системата, общо решение може да се запише като
.
Ние решаване на хомогенна система от уравнения.
Матрицата на коефициент има ранг 4 защото
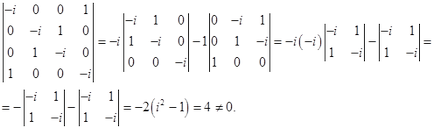
Тъй като в ранг е равен на броя на неизвестните, системата има само тривиално решение,.
Ние решаване на хомогенна система от уравнения.
Матрицата на коефициент има ранг 4 защото
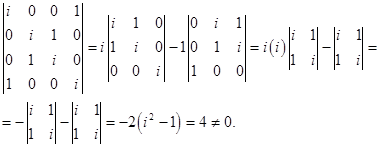
Тъй като в ранг е равен на броя на неизвестните, системата има само тривиално решение,.
По този начин, ние имаме свой собствен вектор и.
Ние избираме като ортогонална базисни вектори ,,,.
Нормализиране намери ортогонална основа:
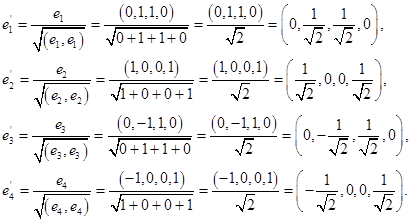
Свързани статии
