Върховенство на умножение на матрици
Да предположим, че два матрица А (m х п) и В (п х л), и на броя на колоните на матрицата А е броя на редовете на матрицата В. След матрица C (m х л) с елементите. (Т.е. I-ия ред на матрицата, умножена по скаларна на й-тата колона на матрицата В, дава ти елемент CIJ на матрицата С, стояща на аз-ти ред и к-тата колона).
. .
Имотът на система от линейни уравнения с тривиален уравнение.
Trivial уравнение - уравнение, в което коефициентите на всички неизвестни и свободни термини са нула.
Теорема: система от линейни уравнения съдържащи тривиално уравнение е еквивалентно на същата система без тривиално уравнение.
Доказателство: Да разгледаме случая (1) и също SLE (2), но не тривиално уравнение.
Нека вектора е решение на системата (1), докато този вектор е решение на (2).
От друга страна, се предполага, че векторът е разтворът на система (2). защото п двумерен вектор, и L е тривиално решение на уравнението, е разтвор (1).
По този начин, системата от линейни уравнения съдържащи тривиално уравнение е еквивалентно на същата система без тривиално уравнение.
Имотът се предлага в допустимия неизвестен SLU
наречена позволено SLU. ако всеки уравнение на системата съдържа поне един позволено неизвестен.
Теорема: Ако е позволено SLE (4), за да даде на свободните неизвестни произволни стойности. т. д .. съществува уникално решение на системата под формата на N-измерен вектор К, който координира стойности, съответстващи свободни неизвестен, са съответно равни.
Заместването в (4). Тогава позволи на неизвестни стойности ще бъдат такива, че:
Т. к. Vector обръща всеки уравнение на системата (4) в точната числова равенство е разтворът на тази система. По този начин, се доказва наличието на разтвори на системата (4).
За да докаже уникалността на такова решение. Нека вектора със същите стойности на неизвестните се предлага като разтвор на (4). След това го замести в (4), получаваме:
Комбинирането на (5) и (6), виждаме, че. По този начин, е доказано, че съществува уникален разтвор на (4) с предварително определени стойности на разположение неизвестен.
1) Тъй като. Безплатни неизвестни стойности може да се настрои безкрайно голям брой начини, системата (4) не е установена.
2) Резолюция SLU винаги съвместими. В този случай тя се определя. ако m = п. т. е. броят на уравнения е равен на броя на неизвестни, и не е определена. ако броят на уравнения е по-малко от броя на неизвестни, т. е. т Решение на системата от уравнения хомогенни Линейно уравнение се нарича хомогенна. ако постоянно план е нула, а в противен случай нехомогенни. Една система, състояща се от хомогенни уравнения се нарича хомогенна и има обща форма: 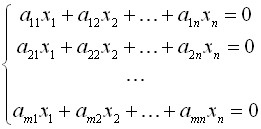
Теорема. Хомогенна система от линейни уравнения има nontrivial решение, ако и само ако рангът й е по-малък от броя на неизвестни.
Доказателство: Да предположим, че системата, чийто ранг е равен. Тя има ненулева решение. Очевидно е, че не надвишава. В случай, че системата има уникално решение. Тъй като системата на еднородни линейни уравнения винаги има тривиално решение, е нула разтвор и това е единственото решение. По този начин, ненулеви разтвори са възможни само когато.
Следствие 1: хомогенна система от уравнения, в които броят на уравненията е по-малко от броя на неизвестни винаги има ненулева решение.
Доказателство: Ако системата от уравнения. ранга на системата е по-малко от броя на уравнения. т.е. , Така, състоянието и, следователно, системата има ненулева разтвор.
Следствие 2: хомогенна система от уравнения с неизвестни има nontrivial решение, ако и само ако му детерминанта е нула.
Доказателство: Да предположим, че система от линейни уравнения хомогенни чиито матрица с детерминанта. Тя има ненулева решение. След това, от теоремата. което означава, че матрицата е дегенерат, т.е. ,
Примери са линейно зависими и линейно независими вектори системи
1) Системата на м двумерен вектори нарича линейно зависими. Ако системата на линейни уравнения (1) има ненулеви решения. Ако системата (1) има не ненулеви разтвори, тази система на вектори е линейно независими.
2) м двумерен вектори, наречени линейно зависима система. ако има ненулев вектор. че има линейна връзка (2). Ако съотношението на всякакъв вид (2), че. системата на вектори се нарича линейно независими.
Примери за линейни програмни проблеми: изход, диета, транспорт, портфейл от ценни книжа.
Свързани статии
