Крайността на алгоритъма

Клонове (дял на G в подгрупи). слагам

8. крайността на алгоритъма. Крайността на алгоритъма следва от крайността на комплекта Г.

При търсенето на клон-и-свързан алгоритъм за решаване на проблема се разбира, с дървовидна структура на оптималните решения и използване на резултатите от задачите за оценка решения. Дървовидна структура обикновено известен като един клон.

Ефективността на клон и свързания алгоритъм се определя от броя на решават проблеми. Решение се състои от два основни етапа. Първият етап е оптималното решение (или близо към него). През втория етап, доказателство за оптималност на решението. Втората стъпка обикновено отнема от първия повече време. Това означава, че броят на подзадачи да се реши да се получи оптимално, може да бъде значително по-малко от броя на подзадачи да бъде решен, за да докаже оптималност.

2. Отчет за проблема с пътуващ търговец

Класически търговски пътник проблем (TSP) е формулиран, както следва: има пълен претеглена насочено графика без бримки G с връх набор N =; теглата на всички дъги са не-отрицателни; В тази графа се изисква да се намери Hamiltonian цикъл на минимално тегло.

Обща информация за ZK изглед представени под формата на размер NxN матрица. S =, където Сий - тегло дъга (I, J) на графиката G, I =. J =. аз ≠ й; Всички елементи на главния диагонал на матрица S са нули.

В типичен интерпретация на горния 1, 2, ..., N на графиката G - този град. Дъгите представляват възможни преходи елементарен. Продавач, първоначално намира в 1, което трябва да получи около останалата част на града, посещение на всеки един от тях само веднъж, а след това се върнете към града 1. теглата на дъгите на графа се интерпретират като дължината на съответните елементарни преходи. Задължително да се намери минималната дължина като валиден (т.е., отговаряща на изискванията на пари в брой), по маршрута на търговския пътник. Като се вземат предвид други възможни интерпретации, изискване симетрия матрицата S е наложено не е от съществено значение, и неравенството на триъгълника.

3. Проблемът с пътуващ търговец на базата на динамично програмиране

Една от основните алгоритми TSP решение въз основа на принципа на динамичното програмиране. В представянето на този алгоритъм ще се придържат към условията, отговарящи на стандарт тълкуването на проблема.

Нека аз - случаен град (и # 206; N), а V - всяко подмножество на места, които не съдържат един град и град аз. Нека M (I, V) означаваме множеството на пътища, всеки от които започва в I, се допълва в 1 и се простира само като междинни продукти чрез определени градове V, навлизаме в всеки един от тях само веднъж. Чрез B (I, V) означават дължината на най-късата пътека определя М (I, V). За решаване на проблема в (I, V) - Белман функция. Както е видно, B (1) - минималната необходима дължина на прост (не самостоятелно кръстовища) от затворен пътя преминаване през всички градове.

Ако V - сек набор, V =, където й ≠ 1 и к ≠ I, тогава набор M (I, V) се състои от един път μ = (I, J, 1). следователно

аз # 206; N, J # 206; , J ≠ т. (1.1)

Да приемем, че стойността на функцията B (I, V) за всичко, което # 206; N \ и всички възможни к-елемент (к

(1.1) - (1.12) - повторение отношения на динамично програмиране за решаване на проблема пътуващ търговец, те гарантират изпълнението на обратния метод Белман. Изчислителната сложност на проблема е, където C - произволна константа (C> 0), п - броят на градовете.

Пример 1.1 За решаване на проблема на пътуващ търговец определено матрица:

Първо, като се използва формулата (1.1), се определят стойностите на B (I,):

В (2) = 5 + 6 = 11; B (3) = 2 + 2 = 4; В (4) = 5 + 2 = 7;

В (2) = 2 + 1 = 3; B (3) = 1 + 1 = 2; В (4) = 4 + 6 = 10.

Освен това, с формула (1.2) последователно се получи (от лявата страна на всеки от следните уравнения съхранява стойности на параметрите са разпределени й, която се осъществява при изчисляването посочено в дясната част (1.2) минимум):

В (2) = минути [S23 + B (3); S24 + В (4)] = минути (5, 2 + 2 + 10) = 7;

В (3) = минути [S32 + B (2,<4>); S34 + B (4<2>)] = Min (2 + 3, 1 + 7) = 5;

В (4) = минути [S42 + B (2,<3>); S43 + B (3,<2>)] = Min (5 + 11, 4 + 4) = 8;

= Min (4, 7, 3, 5, 4 + 8) = 8.

Така, оптималната стойност на критерия в този пример е осем.

Дава възможност да се определи оптималното разпределение на маршрута. Той е както следва:

За да напишете отношения, която се осъществява пряк метод Белман, ще въведем нов формат. Нека M "(V, и) - набор от пътеки, всяка от които започва в 1 комбинация като междинни продукти само от град подмножество V, влизащи в всеки един от тях само веднъж и завършва в I; Тук, както и преди, аз - случаен град (и # 206; N), и V - всяка подгрупа на N, не съдържащ места 1 и аз. Дължината на най-краткия път на M "(V, I) обозначи B * (V, I). Както е видно, B * (1) - минималната необходима дължина на прост (няма самостоятелно кръстовища) от затворен пътя, който минава през града. Ако V - сек набор, V =, където й ≠ 1 и к ≠ аз. след това набор от М "(V, I) се състои от един път μ = (1, J, I). следователно

Да предположим, че стойността на функцията * (V,) за всичко, което # 206; N и всички възможни к-елемент (к

Уравнения (1.3) - (1.4) - повторение отношения на динамично програмиране за решаване на класическия проблем пътуващ търговец, за гарантиране на прилагането на прекия метод на Белман.

Пример 1.2 директен метод броене за решаване на проблема пътуващ търговец, определена от матрицата:

(Забележете, че матрица S в този пример е същият, както в предходните).

Първо, като се използва формулата (1.3), се определят стойностите на B * (, I):

B * (3) = 4 + 5 = 9; B * (2) = 3 + 2 = 5; B * (2) = 4 + 5 = 9;

B * = 4 + 2 = 6 (4.); B * = 3 + 1 = 4 (4.); B * (3) = 4 + 4 = 8.

Освен това, с формула (1.4) последователно се получи (от лявата страна на всеки от следните уравнения съхранява стойности на параметрите са разпределени й, която се осъществява при изчисляването посочено в дясната част (1.4) минимум):

B * (4) = минути [B * (3) + S34; B * (2) + S24] = минути (1 + 9, 5 + 2) = 7;

B * (3) = минути [B * (4) + S43; B * (2) + S23] = минути (4 + 6; 9 + 5) = 10;

B * (2>) = минути [B * (4) + S42; B * (3) + S32] = минути (4 + 5; 8 + 2) = 9;

Така, оптималната стойност на критерия в този пример е осем.

Дава възможност да се определи оптималното разпределение на маршрута. Той е както следва:

4. търговски пътник проблем чрез клон и пътуващ

Друг алгоритъм за решаване на проблема, пътуващ търговец е методът на клонове и граници. По същество това е модификация на изчерпателен търсенето на разтвори, оптимизираните дължи на факта, че определени критерии са нарязани на множество под-оптимална сортиране.

Формално построена дърво от възможности, като се започне от корена. В основата на необходимостта да се даде горните и долните граници. Други отрасли. По-малкият фрагмент от дърво трябва да се изгради, толкова по-успешни бранша натоварване и свързан метод.

Ние имаме следните определения:

Сегашният рекорд - най-големият от получена по време на изпълнението на метода по-ниски граници.

Vertex се нарича мъртва, ако горната граница в нея не превишава текущия запис. Извършване на допълнително разклоняване тя е безполезна.

Терминалът е връх в които горните и долните резултати мач.

Top, разклоняване, които вече са изпълнени, се нарича затворена.

Блузи, които не са мъртви, терминал или затворен, се наричат отворени. Освен това разклонение от тях правят.

Решението приключва, когато опциите в нашето дърво не са отворени капаци. Оптималното решение би било текущия запис.

Горна граница се определя с помощта на "алчни" алгоритъм.

В алчни алгоритъм - алгоритъм за намиране на най-късото разстояние от избора на най-краткия, но избран ръб, при условие, че не се образува цикъл с вече избрани ръбове. "Алчни", този алгоритъм се нарича, защото последните стъпки трябва да плащат тежко за алчност (последната ръба обикновено е най-големият или в близост до дължината).

Стратегия: "Иди до най-близката (които все още не са влезли) град." Да вземем например мрежата на фиг. 2, което представлява тесен диамант. Нека продавачът започва от 1. "Отиваш най-близкия град" алгоритъм ще го отведе до града 2, след това 3, а след това 4; последната стъпка ще трябва да плащат за алчността, обратно на дългия диагонал на ромба. Резултатът ще бъде не най-краткия, а дължината на обиколката.

За изчисляване на долната граница, първо обобщим минималните елементи в редове и колони, а след това изберете от сумите, получени най-великият, но трябва да се вземат под внимание на конфликта.

Пример 2.1 За да се реши от клон и Bound пътуване продавач проблем, определени от матрицата:

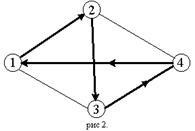
1. Изчислява горните и долните граници в корена:

Горна граница се изчисли, като се използва така наречената "алчни" алгоритъм: всеки преход от този начин в най-близкия град. Изтеглете упътвания:

1 2 ® ® ® 3 4 5 ® ®1

Общата стойност на този маршрут е 12, той определя горната граница в зародиш.

За да изчислим долната граница, първо обобщим минимални елементи в редове и колони, а след това изберете размера на получения-великият:

Редове: 2 + 1 + 2 + 2 + 2 = 9

Чрез Колони: 2 + 2 + 3 + 1 + 2 = 10

Изберете най-много 10 стойности и изберете.

Нека да анализираме колоните: ние можем да преминат към 2 (конфликта). Следователно по-ниска граница е равна на 10 + 2 = 12.

Като резултат от решаването на проблема, а след това ние не се разклони, много. Пишем най-добрия маршрут продавач:

Следователно, проблемът е решен.

Практика създава някога нов проблем оптимизация и тяхната сложност расте. Тя изисква нови математически модели и методи, които позволяват присъствието на много критерии, провеждат глобална търсене на оптимума. С други думи, жизнените сили, за да се развиват математически формализъм оптимизация.

Real Application дискретна проблем оптимизация е много сложна. Съвременни методи за оптимизация не винаги се справят с решаването на реални проблеми без помощта на човека. Не, не е теория, която ще даде възможност за всяка конкретна функция, описваща изявлението на проблема. Следва да се даде по такъв начин, че е по-лесно да се управлява в процеса на решаване на проблема.

библиография

1. Белман, R. Dynamic програмиране - М. Wiley, 1960.- 400 стр.

2. Белман, R. Приложение на динамично програмиране - М. Наука, 1965 - 457 стр.

4. Р. Белман и S. Драйфус приложения на динамично програмиране - АМ 1965 460 стр.

Клонове (дял на G в подгрупи). слагам

Информация за работата на "метод и схема за програмиране клонове в процеса на решаване на проблемите на дискретна оптимизация"

Свързани статии