"Веднъж ми предложиха задачата на острова, който се намира в град Кьонигсберг и е заобиколен от река, която се измерват чрез седем мостове. Въпросът е дали някой непрекъснато около тях може да стане само веднъж на всеки мост. И тогава бях информиран, че един но все още не можех да го направя, но никой не е доказал, че е невъзможно. въпросът е, макар и банална, ми се струваше, обаче, да отбележим, че за решението му не са достатъчни или геометрия или алгебра или комбинаторна изкуство ... след дълго обмисляне, аз н беше лесно правило въз основа на доста убедителни доказателства, че може да се използва във всички проблемите на този вид веднага се определи дали има може да бъде извършено от обход през някакъв номер и по някакъв начин подредени мостове, или не може. Кьонигсберг мостовете са подредени така, че тяхната може да бъде представена на фигурата [Фигура 1], в която а означава остров, б, CID -. на континента, разделени от Bayou Седем мостове са означени с буквите а, в, с, D, е, F, G " ,
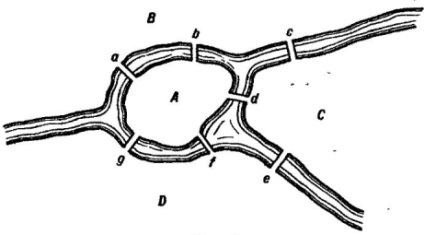
По отношение на този вид открил, че е в състояние да реши проблема Ойлер пише [виж. [5], стр. 102-104]:
"Това решение по своя характер, изглежда да има малко общо математика, и аз не разбирам защо трябва по-скоро от математика да се очаква това решение, а не от всяко друго лице, тъй като това решение е подкрепено от само един аргумент, както и че не е необходимо да се включат за намиране на решения, че всички закони, свързани с математиката. Така че, аз не знам как се оказва, че въпросите, имат много малко общо с математиката, а се оставя да математиката, отколкото други. "
Така че е възможно да се заобиколят Кьонигсберг мостове, минавайки само веднъж през всеки един от тези мостове? За да намерите отговор, ние ще продължим да писмото Ойлер Marinoni:
0 "Въпросът е как да се определи My правило води до следния адрес този въпрос първо място, трябва да се търси, тъй като има участъци, разделени по вода, е възможно да се получи около всички седем мостове, преминава през всеки само веднъж, или не може, .. - тези, в които няма друг преминаване от една към друга, освен чрез моста в този пример четири такива части -. а, в, с, D. освен това е необходимо да се разграничи дали броят на мостове, водещи до тези отделни области, дори или нечетен . по този начин, в нашия случай, на частта а пет мостове, и към остатъка ... Th - три от моста, т.е. броя на мостове, водещи до отделните участъци, странни, и че сам е достатъчно за решаване на проблема, когато той е решен да се прилага следното правило: ако броят на мостове, водещи до всеки отделен сайт, това е още , а след това обход въпросната би било възможно, и в същото време бихме могли да започнете обиколката на всяка зона. Ако някой от тези номера, два ще бъде странно, тъй като само един да е странно, не, дори и след това мога да направя прехода, както е предписано, но само в началото на заобикаляне трябва задължително Той се приема от една от двете места, което е нечетен брой мостове. Ако най-накрая, имаше повече от две области, които са с нечетен брой на мостове, а след това подобен ход е невъзможно ... дали е възможно да се даде тук други по-сериозни проблеми, този метод може да бъде на още по-голяма полза и те не трябва да бъдат пренебрегвани " ,
Математик, той пише, че преходът е възможно, ако е част от кръстовището на реката, има само две области, в които провежда нечетен брой мостове. С цел да се направи по-лесно да си представим, че ще изтрие цифрата вече е отминал мостовете. Лесно е да се види, че ако започнем да се движат в съответствие с правилата на Ойлер, пресече един мост и да го изтриете, а след това цифрата ще се появи станция, където отново има не повече от две области, които са с нечетен брой на мостове, както и наличието на региони с нечетен брой мостове, ще бъдат разположени в един от тях. Продължаване и т.н., проверете всички мостове само веднъж.
Историята на мостовете на град Кьонигсберг е модерен продължение. Open, например, училище математика книга под редакцията на Н. Vilenkin за шести клас. В него на страница 98 в категорията на грижи и изобретателност ще намерите проблема, пряко свързани с тази, която се използва, за да бъде решен с Ойлер.
Задача № 569. езеро е седем острови, които са свързани помежду си, както е показано на фигура 1.2. На какво острова трябва да предостави на пътуващите с кораб, че те да могат да прехвърлят всеки мост и само веднъж? Защо не може да достави пътуващи до остров A?
Решение. Тъй като тази задача е подобен на проблема с мостовете на Кьонигсберг, когато решението си, ние също да използват правилото Ойлер. В резултат на това, ние получаваме следния отговор: лодката трябва да достави всички посетители на остров Е или F. така че те да могат да преминат на всеки мост веднъж. От същата Ойлер правила трябва да е невъзможно да се заобиколят се изисква, ако започне от остров А.
В заключение, ние отбелязваме, че проблемът с Кьонигсберг мостове и други подобни задачи, заедно с набор от методи за изучаване ги направи много важно от практическа гледна точка, клон на математиката, наречен теория на графите. Първата работа на колоните принадлежи на Ойлер и се появява през 1736. По-късно графики работихме Кьониг (1774-1833), Хамилтън (1805-1865), на съвременната математика - Berge, О. руда, Zykov.
Свързани статии
