Свойствата на основните линейни програмни проблемите, свързани с качествата на изпъкнали множества.
Наборът от точки нарича изпъкнала, ако заедно с две точки съдържа изпъкнала и тяхното произволна комбинация.
Геометричната смисъла на това определение е, че на снимачната площадка, заедно с изцяло притежаваните от произволни точки, а отсечката, която ги свързва. Примери изпъкнали множества са праволинейни сегменти, полуравнина, кръг, сфера, куб, наполовина и др.
Ъгловите точки на изпъкнала зададена точка наречените не-изпъкнала комбинация от две произволни точки на комплекта. Например, правоъгълен триъгълник точки са върхове, кръг - точка кръга, че нейната граница.
Много от основните задачи на линейни планове за програмиране е изпъкнал (ако не е празна). Non-празен набор от планове се нарича полихедронов решения, както и всяко кътче на решения полихедронов точка - най-добре.
Ако основният проблем на линейното програмиране е оптималният план, целта функция на проблема се максималната стойност на един от върховете на решенията. Ако максималната стойност се постига повече от един връх, обективната функция получава във всяка точка е изпъкнала линейна комбинация от тези върхове.
Непразна набор от планове, основният проблем на линейното програмиране образува изпъкнал Стол, всеки връх, който определя основния план. За един от референтните планове (т.е., един от върховете на разтвори многостен) обективната функция е максимална (приемайки, че функцията е ограничена от горе на набор от планове).
Върховете на решенията, в които целевата функция достига максималната си стойност, е възможно да се намери съвсем проста, ако проблемът е в стандартния формуляр не съдържа повече от две променливи:
Пресечната точка на половин равнини, определени от система от линейни неравенства наречените решения (HR) система, както и, ако отговаря на условията на не-негативност. той се нарича областта на изпълними решения (СДТ).
Ако системата е съвместима неравенства, района на изпълними решения на проблема е изпъкнало множество, което се нарича полигон решения. Страните на многоъгълник лежат върху линии, чиито уравнения са получени от оригинала
системни ограничения, като заменя знака на неравенството на знака за равенство точна.
Решаването на задачи на линейното програмиране геометрична метод се състои от следните стъпки.
1. На самолета, построен направо, което уравнения са получени чрез замяна на знака на неравенството в ограниченията за знака за равенство точна.
2. Намерете половин равнината, определена от всяка от ограниченията на проблема.
3. Изграждане на полигон решения.
4. Изграждане на вектор, който показва посоката на увеличаване на целевата функция.
5. Изграждане на първоначалната целева функция директно и след това се премества успоредно на себе си в посока на вектора на крайната точка на ъгъл от разтворите на полигон на. В резултат на това, намирането на точката, в която целевата функция се приема максималната стойност, или множество от точки, с една и съща максималната стойност на целевата функция на оптимална алтернатива, ако стартовата линия се слива с една от страните на процеса на вземане на полигон, или да зададете началото безгранична функцията на набор от планове.
6. Определяне на координатите на точката на максимална функционалност и изчисляване на стойността на целевата функция в този момент. Минималната стойност на обективната функция е линейно движение от първия ред в посока, обратна на вектора.
Пример 1. Намери максимум и минимум на линейна функция
Решение. Ние изграждане на многоъгълник вземане равнина (фиг. 1). За да направите това, в неравенството в системата на ограниченията и условията за не-негативност на променливите неравенство знаци ще замени глоба знак за равенство.
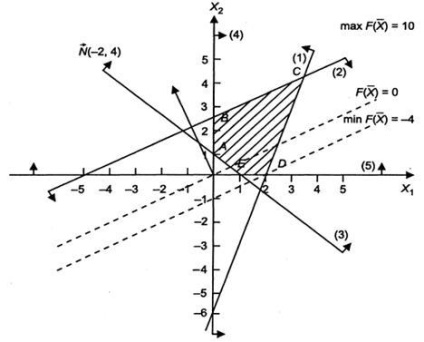
Фигура 1. Конструкция на разтвори многоъгълник
Построен система, ние откриваме съответния период на самолета, както и тяхното пресичане.
Решения на многоъгълник е петоъгълник ABCDE, точки, чиито координати удовлетворяват неравенството в променливи и ограниченията за неотрицателност на проблема на системата.
За да намерите екстремални точките на първоначалната конструкция и директно вектор (-2, 4). Преместването направо в посока на вектора, открие точка С, в който първоначалното линия приема позицията на базовата линия. Следователно, в точка С цел функция има максимална стойност. След точка В се получава чрез пресечната точка на линиите 1
и 2 на системата, нейните координати удовлетворяват уравненията на тези редове:
Решаването на системата от уравнения, получаваме: = 3.4; = 4,2; където намираме максималната цел функция стойност = (- 2) * 3,4 + 4 * 4,2 = 10.
Чрез хипотеза, първоначалният проблем е успоредна права линия (2), тъй като коефициентите на променливите. пропорционална (-2) / (- 1) = 4/2 = 2. Следователно, първоначалното положение на референтния правата линия се в точки В, С, и навсякъде в сегмент BC, което предполага същата максимална стойност. За определяне на координатите на точка Б решаване на системата от две линейни уравнения:
Максималната стойност на целевата функция в точка Б е равен на:
Пишем снимачната площадка на оптимални решения като линейна комбинация от изпъкнали ъгли сегмента BC пунктове, когато има.
Чрез заместване на координатите на ъгловите точки, получаваме:
Заместването на всяка стойност между 0 и 1, ние получаваме координатите на множеството сегмент BC точки на всеки от които обективната функция предполага максимална стойност, равна на 10.
За да намерите минималната стойност на целевата функция на проблем първоначалното движение направо в посока, противоположна на вектора. Стартовата линия приема позицията на базовата линия на връх D, където к = 2, = 0, и минималната стойност на обективната функция е: = (- 2) * 2 + 4 * 0 = -4.
Пример 2: геометричен метод за решаване на проблеми линейни програмиране от примера на задачата и конструиран модел на бизнес предприятие, представени в раздел 2.2.1.. Тъй като моделът има само две променливи,
след това този проблем може да бъде решен чрез геометрична метод.
Изграждане на самолета (фиг. 1), многоъгълник на възможните решения на проблема. За да направите това, в неравенството в системата на ограничения по отношение на неравенството знаци замени точните признаци равенство:
Конструиране получава ограничаване директно намери съответната половина равнина на допустимите стойности на променливите и след тяхното пресичане (фиг. 1).
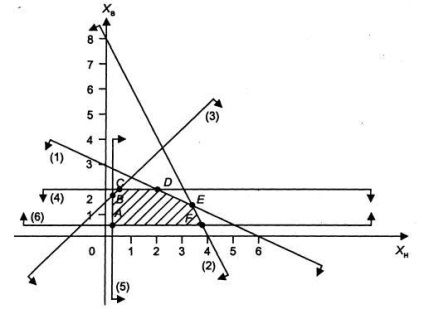
Фиг.1 Изграждане на района на изпълними решения
Посока стрели от всяка гранична линия се определя чрез директно заместване в координатната неравенството произволно избрани точки, например, (0, 0), а когато удовлетвореността на неравенството в посоката на стрелката цел контролно-пропускателен пункт в противен случай - напротив.
Полученият разтвор пространство има многоъгълник ABCDEF.
Corner решения полигон точки имат следните координати:
А (0,25; 0,5), В (0.25, 1.75), C (0.5, 2), D (2, 2), E (3: 1), F (3,75 0.5).
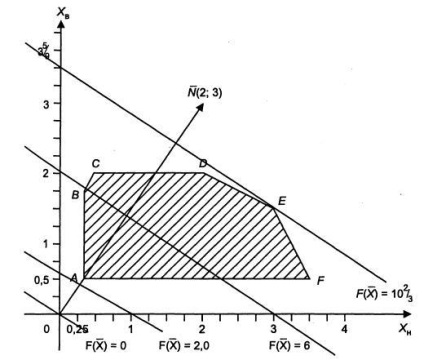
За минимума и максимума на обективната функция и конструиране на първоначалния вектор градиент директно (2; 3) (фигура 2). Координати на вектора са линейни коефициентите на целевата функция променливи. За да се конструира графиката на обективната функция дадена произволна стойност Ако = О, линия преминава през началото. За изграждането му, определяне = 1, се получи = -2/3 и к = 1, се получи = -3/2 (фиг. 2). Ако приемем = 6, по същия начин линията конструиране на обективната функция.
Тогава за = 0.25 и = 0,5 определи минималната стойност = 2. По този начин, графиката се конструира серия от паралелни линии (фигура 2)., При което вектор градиент (2, 3) показва посоката на растеж на обективната функция.
Максималната стойност ще бъде в точка Е. От точка Е се получава чрез пресечната точка на линиите (1) и (2), тогава координира opredeleniyaee решаването на системата от уравнения:
Максималната стойност на целевата функция
Обективната функция пресича оста на мястото =. и в точка = ос.
Свързани статии
