Дефиниция на двоен интеграл
Нека самолет $ \ mathbf> $ бъде ограничена затворена област $ \ mathbf> $ с по части гладка граница, и нека в областта $ \ mathbf> $ дефинира функция $ \ mathbf на> (\ mathbf> $, $ \ mathbf>) $ ,
Ние разделяме област $ \ mathbf> $ произволно на $ \ mathbf> $ поддомейни $ \ mathbf> _ $, $ \ mathbf> _ $, $ \ mathbf> _ ,, \ mathbf> _ $ ,. Символ $ \ mathbf> (\ mathbf> _) $ ще означаваме района на област $ \ mathbf> _ $; символ $ диаметър (\ mathbf>) $ тук и ще продължи да бъде на максимално разстояние между две точки, принадлежащ към поле $ \ mathbf> $: $$ диаметър (D) = \ mathop \ limits_ \ Rho (P_1, P_2); $$ символ $ г $ означаваме най-големият от диаметъра на $ \ mathbf> _ $: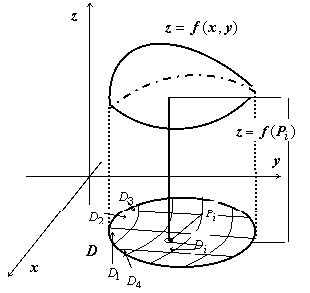
Ако граница последователност с интегрални суми
$ D = \ mathop \ limits_ диаметър (D_i) \ до 0 $, зависи нито от метода на разделяне на полето $ \ mathbf> $ на поддомейн $ \ mathbf> _ $, нито избора на точки $ \ mathbf> _ $, след това функцията $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ се нарича интегрируеми поле $ \ mathbf> $, но стойността на тази граница се нарича двоен интеграл от функцията $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ на полето $ \ mathbf> $ и е обозначен $ \ iint \ limits_D $.Ако боядисате стойност $ \ mathbf> (\ mathbf>) $ чрез координатите на $ \ mathbf> $ и до $ \ mathbf> $ като $ \ mathbf> = \ mathbf> $, да получат друго предназначение на двойна неразделна: $ \ iint \ limits_D $. Така че, накратко,Теоремата за съществуване на двойното неразделна
Ако подинтегрален $ \ mathbf> (\ mathbf> \ mathbf>) $ е непрекъсната по поле $ \ mathbf> $, то тогава е интегрируеми на терена.
Геометричната смисъла на двойния интеграл. Геометричната смисъла на всеки термин на интегралната сумата
От геометрична гледна точка на неразделна сумата от представлява сумата на обемите на цилиндъра с бази $ S (D _) $ височини и $ е (P_i) $.
Ако $ е (х, у) \ geqslant 0 $, след $ е (P_i) \ cdot S (D_i) $ - обем на право цилиндър с> _ $ височина $ \ mathbf база $ \ mathbf> (\ mathbf> _) $ ; всички неразделна сума $ \ сума \ limits_ ^ п $ - сумата от обемите на цилиндъра, т.е. обемът на тялото на стъпка - височината на стъпка над поддомейн $ \ mathbf> _ $, равен на $ \ mathbf> (\ mathbf> _) $. Когато $ D = \ mathop \ limits_ диаметър (D_i) \ до 0 $, този етап на тялото се доближава до този, показан в тялото на фигурата, ограничена отдолу площ от $ \ mathbf> $, най - повърхност $ \ mathbf> = \ mathbf> ( \ mathbf> $, $ \ mathbf>) $, с цилиндричната странична повърхност на указание, което е на границата на $ \ mathbf> $, успоредно на оста и генераторите $ \ mathbf> $. Двойна неразделна $ \ iint \ limits_D $ равно на обема на тялото.Вижте също:
Surface неразделна от първи вид и неговите свойства
Механична прилагане на линия интеграл от 1-ви вид
Инвариантна определение на разминаване
Механично прилагане на троен интеграл
Напред към съдържанието на $ \ стрелкаНадясно \ стрелкаНадясно \ стрелкаНадясно $
Свързани статии
