Има безкрайно много елементи, от които не може да се преномерират. Тези комплекти са наречени безброй.
теорема на Кантор. Наборът от всички точки на сегмент [0, 1] несметен.
Нека определените точки на сегмент [0, 1] е изброимо. Следователно, тези точки могат да бъдат изброени, т. Е. разположен в последователност форма x1. x2 ... хп. ....
Разделете интервала [0, 1] в три равни части. Където и точка x1 на. то не може да принадлежи на всички сегменти. , , Ето защо, някои от тях са D1 сегмент. не съдържа точка x1 (фиг. 1.7). Вземи това парче D1 и го разделете на три равни части. Сред тях, винаги има един сегмент от D2. не съдържащ точка x2. Ние разделят интервала на три равни части, и така нататък. Е. Получаване на последователност от сегменти D1 É D2 É D3 É...ÉDn É.... Чрез Cantor аксиома клони към точка х с п ® ¥. Чрез строителството, тази точка х принадлежи на всеки сегмент D1. D2. D3, ..., Dn. ..., т. Е. Това не може да съвпада с всяка една от X1 на точки. x2, ... хп. ..., т. Е. Последователността на x1. x2 ... хп. ... не обхваща всички точки на интервала [0, 1], което противоречи на първоначалното предположение. Това доказва теоремата.
Определете еквивалентни на множеството от всички точки на сегмент [0, 1] е зададен континуум.
Тъй като множество интервали от точки, линии и цялата линия еквивалент един до друг, всички те имат кардиналност на континуум.
За да докаже, че множеството има кардиналност на континуум, е достатъчно да се посочи едно към едно съответствие между този набор и поставените точки на сегмента, или на цялата линия интервал.
Фиг. 1.8 че множество точки на у парабола = х 2 еквивалентни на определени точки на линия - ¥ 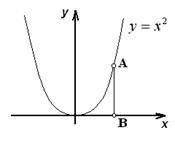
Задайте кардиналността на континуум, можете да използвате и следната теорема на кардиналността от наборите на континуум (представен без доказателства).
ТЕОРЕМА 1. Множеството от всички подгрупи на снимачната площадка на броим броим.
Теорема 2. Наборът от ирационални числа има кардиналност на континуум.
Теорема 3. Наборът от всички точки на n-мерното пространство за всеки п има кардиналност на континуум.
Теорема 4. Множеството от всички комплексни числа има кардиналност на континуум.
Теорема 5. Комплектът на непрекъснатост определени за интервала [а. Ь] има кардиналност на континуум.
По този начин, силата на безкрайни серии може да варира. Силата на континуум е по-голяма от силата на изброимо множество. Отговорът на въпроса дали има множество по-висока мощност, отколкото силата на континуум, следната теорема (при положение, без доказателство).
Теорема на по-високите енергийни набори. Множеството от всички подгрупи на даден набор има по-висок капацитет от тесте.
От това следва, теорема, че не съществува наборите с възможно най-висока мощност.
Тестовите въпроси към темата 1
1. Нека за Î А. Следва ли, че> A?
2. В този случай, АА ÇВ?
3. името на набора, който е подмножество на всеки набор.
4. Може да бъде най-различни, съответстващи на нейната подгрупа?
5. Силата на набор от вече: набор от естествени числа, или множество точки на интервала [0, 1]?
Свързани статии
