Ние доказваме, че $ MN || AD \ и \ MN = \ Фрак $.
Помислете за вектор $ \ overrightarrow $. Ние се използва в по-общ полигон за допълнение вектор. От една страна, ние откриваме, че
От друга страна
Поставянето на последните две равенства, получаваме
От $ M $ и $ N $ - средата на страните на трапеца, тогава имаме
От същата равенство (от $ \ overrightarrow $ и $ \ $ overrightarrow една и съща посока, и по този начин, лежат на една права), че $ MN || АД $.
Примери за цели за трапец на концепция средната линия
Страните на трапец са 15 $ \ см $ и 17 $ съответно \ $ см. Периметърът на трапец е равна на $ 52 \ см $. Да се намери дължината на средната линия на трапеца.
Да означим средната линия на трапеца от $ N $.
Сборът от двете страни е равна на
\ [15 \ см + 17 \ см = \ cm \ 32]
Следователно, тъй като периметърът е равно на $ 52 \ $ см, размерът на база е
\ [52 \ 32 см \ см = 20 \ cm \]
Следователно, от Теорема 1, получаваме
Краищата на диаметъра на окръжност изнесен от нейната допирателна съответно до $ $ 9 см и $ 5 $ см. Намерете диаметъра на този кръг.
Да предположим, че са дадени окръжност с център $ O $ и диаметър $ AB $. Ние черпим допирателна $ л $ и изграждане на разстояние $ АД = 9 \ см $ и $ BC = 5 \ $ см. Равен радиус $ ОН $ (фиг. 2).
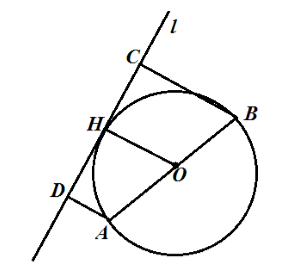
От $ АД $ и $ BC $ - разстояние до допирателната, $ AD \ бот л $ и $ BC \ бот л $ и тъй като $ ОН $ - радиусът, $ ОН \ бот л $ на следователно $ OH | \ лява | AD \ десен || BC $. От всичко това ние виждаме, че $ ABCD $ - трапец и $ ОН $ - неговата средна линия. От Теорема 1, получаваме
\ [D = 2ОН = 2 \ cdot 7 \ cm = 14 \ cm. \]
Свързани статии
