В примерите разисквано по-горе изчислява вероятността от елементарни събития. Възниква въпросът: как да се определи вероятността на дадено събитие, ако знаете някаква информация за събития, които са настъпили с него? [1] Вероятността на събитие в изчислението, която отчита информация за събитието се нарича условно V. и е посочена като P (A | B).
Вероятността на събитие, при условие, че събитието настъпили Б. равна на вероятността за събитие А и В, разделен на вероятността на събитието от:
Вероятността за събитие, при условие, че събитието възникна е вероятността за събитие А и В, разделен на вероятността за събитие:
където Р (А и В) - вероятност за събитие А и Б. Р (А) - вероятността от събитие A. Р (В) - Вероятността за събитие.
Изтеглете бележка в Word или PDF
В действителност, съгласно формула (1) и (2) това стенографски условна вероятност на базата на таблица за извънредни ситуации. Да разгледаме пример, обсъдени в предишна статия (фиг. 1). Да предположим, че ние знаем, ако някои семейство ще си купя широкоекранен телевизор. Каква е вероятността, че това семейство наистина си купите телевизор?

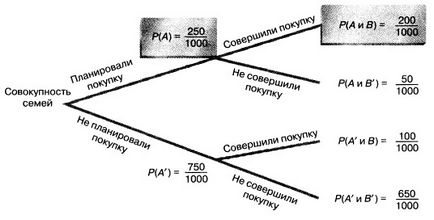
Фиг. 1. Поведение широкоекранни телевизори купувачи
В този случай, трябва да се изчисли условна вероятност P (покупка е направена | покупка планирано). Тъй като знаем, че семейството планира да закупи, пространството на пробата не е вън от 1000 семейства, но само на тези, които планират да купят широкоекранен телевизор. 250 200 от тези семейства всъщност купих този телевизор. Следователно, вероятността, че семейството наистина ще купи широкоекранен телевизор, ако това се предвижда да се изчислява по следната формула:
P (покупка е направена | покупка планирано) = брой на семействата, които се планират и купени широкоекранен телевизор / брой домакинства планирате да си купите широкоекранен телевизор = 200/250 = 0.8
Този резултат дава формула (2):
А там, където събитието е, че семейството планира да купи широкоекранен телевизор, а в случай - че тя наистина си е купил. Чрез заместване на реални данни, ние получаваме формулата:
Фиг. 2. Решение Tree
Например, за да се изчисли вероятността, че семейството ще купи широкоекранен телевизор, ако тя планира да направи това, да определи вероятността на дадено събитие е планирано, и покупката направи. и след това го разделете на вероятността от планираните покупка събития. Преместването на дървото на решенията е показано на фиг. 2, получаваме следното (подобно на предишния) отговор:
В примера за закупуване на широкоекранен телевизор, вероятността, че случайно избрана семейство закупен широкоекранен телевизор, при условие, че тя планира да го направи, тя е 200/250 = 0,8. Спомнете си, че безусловно вероятността случайно избран семейство закупен широкоекранен телевизор, е 300/1000 = 0,3. Това предполага един много важен извод. Приори информация, че семейството планира да закупи, се отразява на вероятността за повечето покупки. С други думи, тези две събития са независими една от друга. За разлика от този пример, има статистически независими събитие, вероятността от които са независими един от друг. Статистическа независимост се изразява идентичността: P (A | B) = P (A). където Р (А | Б) - вероятността на събитие, при условие, че едно събитие се е случило B. P (A) - безусловно вероятността за събитие А.
Имайте предвид, че събитията А и В са статистически независими един от друг, ако и само ако P (A | B) = P (A). Ако таблицата за непредвидени имат размер от 2 х 2, това условие е изпълнено най-малко една комбинация от събития А и Б. Това ще бъде вярно за всяка друга комбинация. В нашия пример, закупуване на планирани събития покупка е направена и не са статистически независими, тъй като информацията за едно събитие се отразява на вероятността от другата.
Помислете за един пример, който показва как да се тества статистическа независимост на две събития. Молим 300 семейства, които са купили широкоекранен телевизор, независимо дали те са доволни от покупката си (фиг. 3). Определяне дали степен на удовлетвореност между покупката и вида на телевизията.
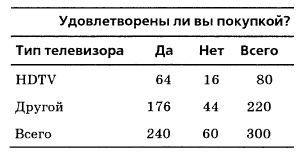
Фиг. 3. Информацията, характеризираща степента на удовлетвореност на клиента широкоекранни телевизори
Въз основа на тези данни,
Р (купувач удовлетворен) = 240/300 = 0,80
Следователно, вероятността, че купувачът е доволен от покупката, както и че семейството е купил HDTV телевизия, равна на една от друга, и тези събития са статистически независими, тъй като по никакъв начин не са свързани.
Умножение правило на вероятностите
Формулата за изчисляване на условната вероятност позволява да се определи вероятността от съвместното събития А и В. решаване на формула (1)
спрямо съвместното вероятност Р (А и В). Ние се получи общото правило за умножение на вероятности. Вероятността за събитие А и В е равна на вероятността на събитие, при условие, че събитието настъпили Б. умножава по вероятността на събитието от:
(3) Р (А и В) = P (A | B) P * (В)
Вземем примера на 80 семейства, които са купили широкоекранен HDTV телевизия (фиг. 3). От таблицата се вижда, че 64 семейства са доволни от покупката си, а 16 - не. Да предположим, че сред тях произволно избрани две семейства. Определете вероятността, че и купувачът ще бъдат удовлетворени. Използване на формула (3), ние получаваме:
Р (А и В) = P (A | B) * Р (В)
А там, където събитието е, че втората семейството е доволни от покупката, както и в случай - че първото семейство е доволни от покупката. Вероятността, че първото семейство е доволни от покупката, равно на 64/80. Въпреки това, вероятността, че второто семейство също е доволен от покупката си, в зависимост от отговора на първото семейство. Ако първото семейство, след като избирателната не се връща на пробата (вземане на проби без замяна), броят на анкетираните, е сведен до 79. Кога беше първото семейство доволни от покупката си, вероятността, че другото семейство също ще се радва, е 63/79, тъй като само 63 останаха в пробата семейства са доволни от покупката си. По този начин, чрез заместване във формулата (3) специфични данни, ние получаваме следната реакция:
Р (А и В) = (63/79) (64/80) = 0,638.
Следователно, вероятността, че са доволни от покупките си и двете семейства, равна на 63,8%.
Да предположим, че след разпита първо семейството се връща в извадката. Определете вероятността, че и двете семейства ще бъдат щастливи с покупката си. В този случай, вероятността, че и двете семейства са доволни от тяхната покупка на същото, и равни на 64/80. Следователно, Р (А и В) = (64/80) (64/80) = 0,64. По този начин, вероятността, че са доволни от покупките си и двете семейства, равна на 64,0%. Този пример показва, че изборът на втория семейството не зависи от избора на първия. По този начин, като се замести в (3) на условна вероятност P (A | B), вероятността P (A). ние получаваме формула умножаване на вероятността от независими събития.
Правилото за умножение на вероятностите за независими събития. Ако събития А и В са статистически независими, вероятността от събития А и В е равна на вероятността за събитие умножава по вероятността от А. случай.
Ако това правило е в сила за събития А и В означава, че те са статистически независими. По този начин, има два начина за определяне на статистическата независимост на две събития:
- Събития А и Б са статистически независими един от друг, ако и само ако P (A | B) = P (A).
- Събития А и В са статистически независими един от друг, ако и само ако P (А и В) = Р (А) P (B).
Ако таблицата за непредвидени имат размер от 2 х 2, едно от тези условия е изпълнено най-малко една комбинация от събития А и Б. Това ще бъде вярно за всяка друга комбинация.
Безусловното вероятността за едно елементарно събитие
където B1 събития. В2. ... Бк са взаимно изключващи се и изчерпателен.
Ние илюстрират прилагането на тази формула, например Фиг.1. Използване на формула (5), ние получаваме:
където P (A) - вероятността, че планирана покупка, P (В1) - вероятността, че е направена покупката, P (В2) - вероятността, че покупката не е направено.
Условната вероятност на събитието дава възможност за информация за това какво се е случило някакво друго събитие. Този подход може да се използва за актуализиране на базата на вероятностите новопристигнали информация, както и за изчисляване на вероятността, че наблюдавания ефект е следствие от някаква конкретна причина. изясняване на процедурата по тези вероятности се нарича теорема на Бейс. За първи път е разработена от Томас Бейс през 18-ти век.
Да предположим, че фирмата, посочена по-горе, ние опознаването на пазара за нов модел телевизор. В миналото 40% от телевизори, създадени от компанията, успех, а 60% не получи моделите за признаване. Преди да обяви освобождаването на нов модел, търговци упражняват контрол върху търсенето на пазара и заснемане. В миналото, на успеха на 80% от моделите, които са получили признаване, прогнозира по-рано, в същото време 30% благоприятни прогнози са правилни. За новия модел маркетинговия отдел даде благоприятна прогноза. Каква е вероятността, че новият телевизорът ще бъде в търсенето?
Теоремата на Бейс "може да бъде извлечена от определението на условна вероятност (1) и (2). За изчисляване на вероятностите P (B | А), да формула (2):
и заместване на мястото на Р (А и В), стойността на формула (3):
Р (А и В) = P (A | B) * Р (В)
Заместването на Р (А) с формула (5), ние получаваме Бейс теорема:
където B1 събития. В2. ... Бк са взаимно изключващи се и изчерпателен.
Представяме следната нотация: S събитието - телевизорът е в търсенето. Събитие S "- телевизорът не е в търсенето. Събитие F - благоприятна прогноза. Събитие F "- с лоша прогноза. Да приемем, че P (S) = 0,4, P (S ') = 0,6, P (F | S) = 0,8, P (F | S') = 0,3. Прилагането на Бейс теорема получаваме:
Вероятността за търсенето на нов модел на телевизия, при условие благоприятна прогноза е 0.64. Следователно, вероятността от липса на търсене, при условие е благоприятна прогноза 1-0,64 = 0.36. Метод за изчисление е показано на фиг. 4.

Фиг. 4. (а) Изчисления с формула Бейс да се оцени търсенето на вероятностите телевизори; (B) дървото на решения в проучването на търсенето на нов модел телевизор
Помислете за пример прилагане теорема на бейс за медицинска диагноза. Вероятността, че човек страда от специфично заболяване, равно на 0.03. Медицински тест позволява да се провери дали това е така. Ако човек е наистина болен, вероятността за точна диагноза (твърдейки, че човек е болен, той е наистина болен), равна на 0,9. Ако човек е здрав, вероятността за фалшиво положителен диагноза (твърди, че на болния, когато е здрав) е 0,02. Да приемем, че медицинско изследване даде положителен резултат. Каква е вероятността, че едно лице е наистина болен? Каква е вероятността на точна диагноза?
Представяме следната нотация: Събитие D - човек е болен. Събитие D "- човек е здрав. Събитие T - положителна диагноза. Събитие Т "- диагнозата е отрицателна. От състояние задача предполага, че P (D) = 0,03, P (D) = 0,97, P (T | D) = 0,90, P (T | D ') = 0,02. Прилагането на формула (6), ние получаваме:
Вероятността за положителен диагностика на човек е наистина болен, е равно на 0,582 (вж. Също фиг. 5). Имайте предвид, че знаменател с формула Бейс вероятност е положителна диагноза, т.е. 0.0464.
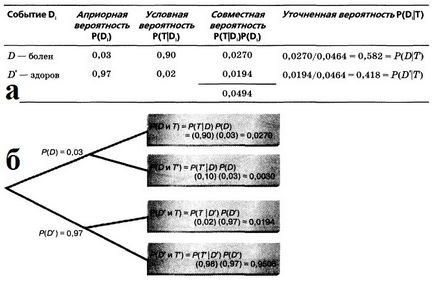
Фиг. 5. (а) Изчисления с формула Бейс за оценка на точността на медицинска диагноза; (B) дърво на решенията, когато се оценява точността на медицинска диагноза
Можете също така да се интересуват от:
Свързани статии
