След като решен това уравнение по отношение на



Помислете за няколко примера, всеки от които ще се представят последователността от стъпки за решаването на проблема с намирането на собствени стойности и собствени.
Намерете най-собствени стойности и собствени
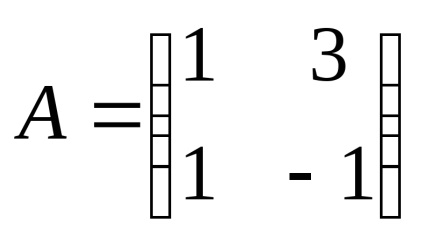
Матрицата е измерение 2

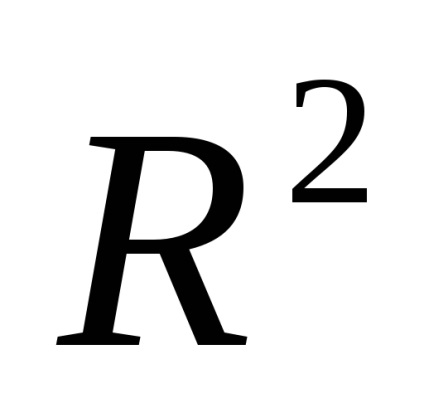
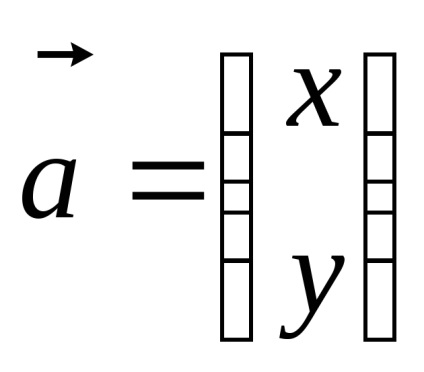
Създаване на уравнението за намиране на собствените вектори във формуляра за матрица:
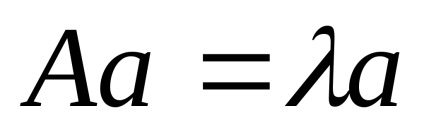

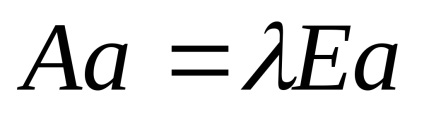

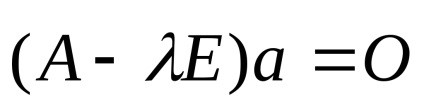
3. презапис уравнението в матрица образуват система от уравнения:
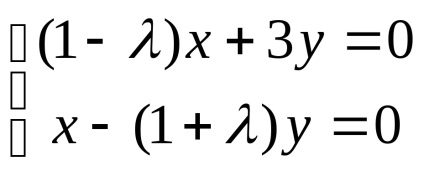
Хомогенна система има nontrivial разтвори, ако и само ако детерминантата на неговата основна матрица е равен на 0. получи характеристика уравнението на системата и решаването:
.
Собствените стойности

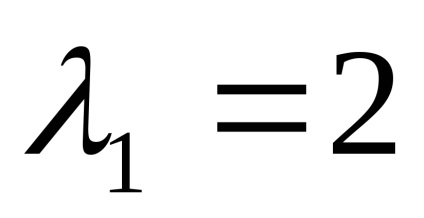
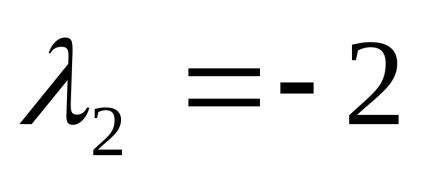
Ние намираме собствените вектори за всеки от своите собствени ценности:
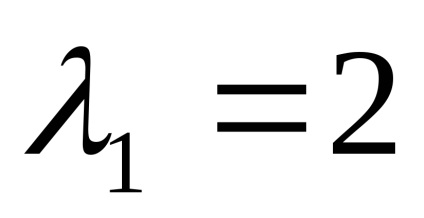
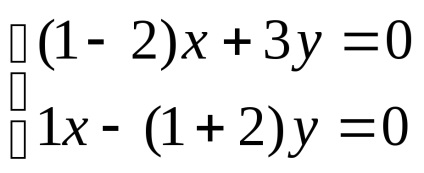
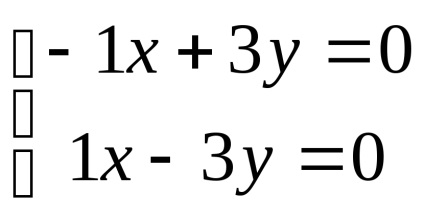
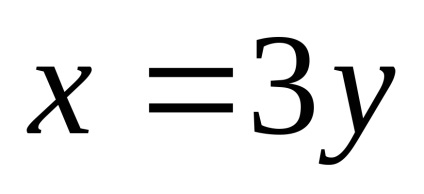
нека
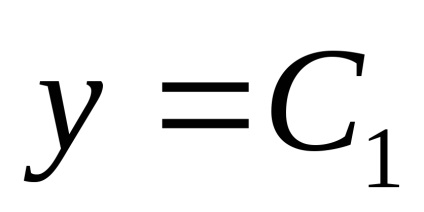

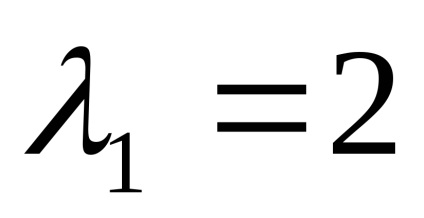
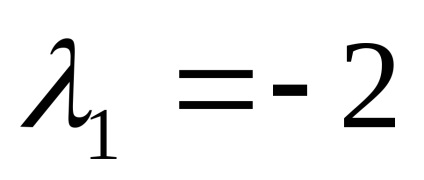
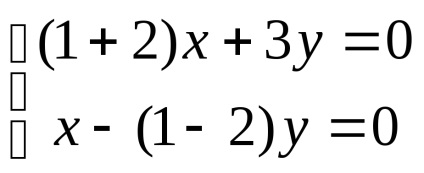
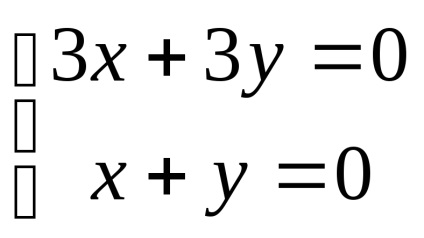
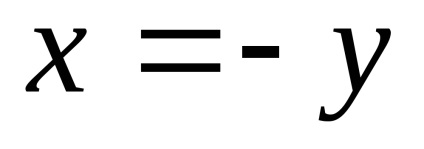
нека
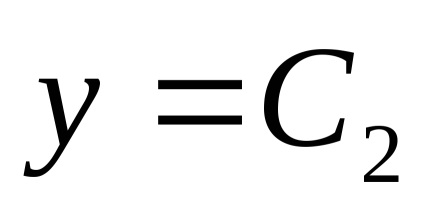

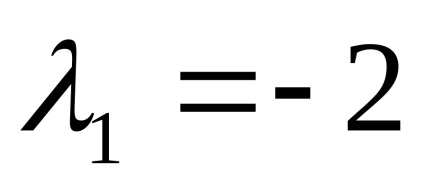
Пример 2. Виж собствените стойности и собствени вектори на оператор линейна. в предварително определен основа matritseyA =
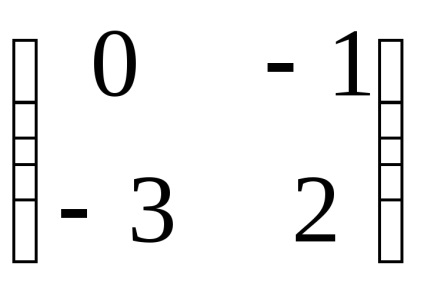
Състав и решаване на уравнението характеристика
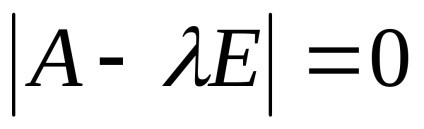
Тогава характеристика уравнението под формата:
,
,
- собствените стойности на линеен оператор.
Ние намираме собствените вектори, отговарящи на собствената стойност
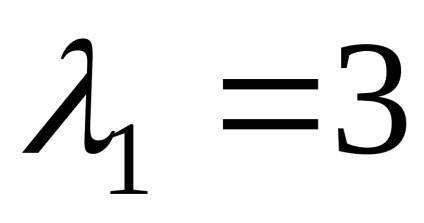
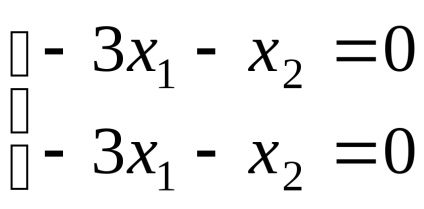
Поставянето в последното уравнение
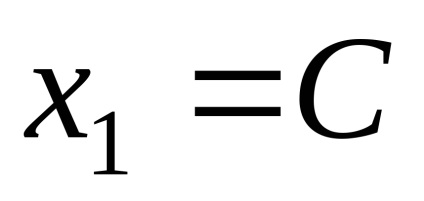
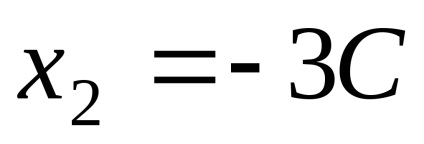
Местоположение собствени вектори, отговарящи на собствената стойност
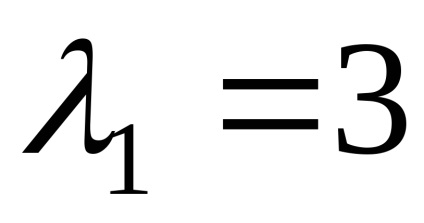
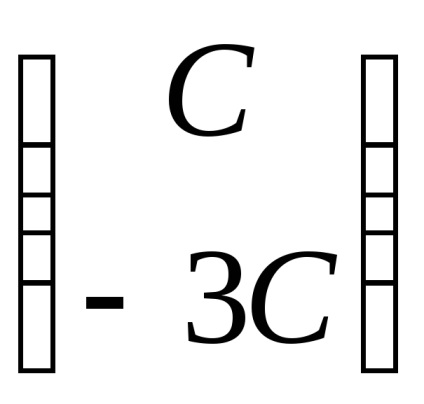
Ние намираме собствените вектори, отговарящи на собствената стойност
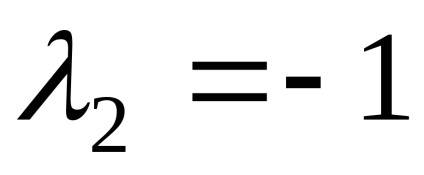
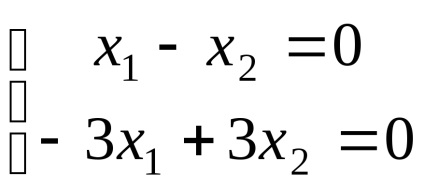
Поставянето в последното уравнение
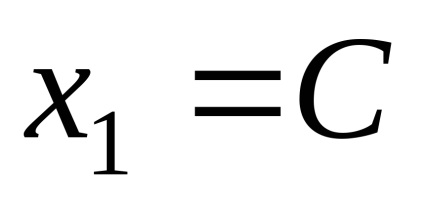
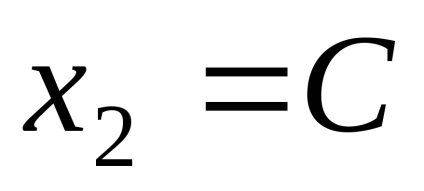
Местоположение собствени вектори, отговарящи на собствената стойност
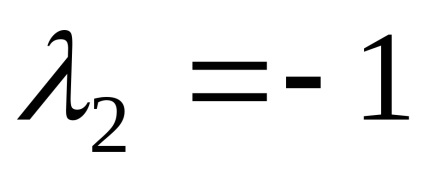
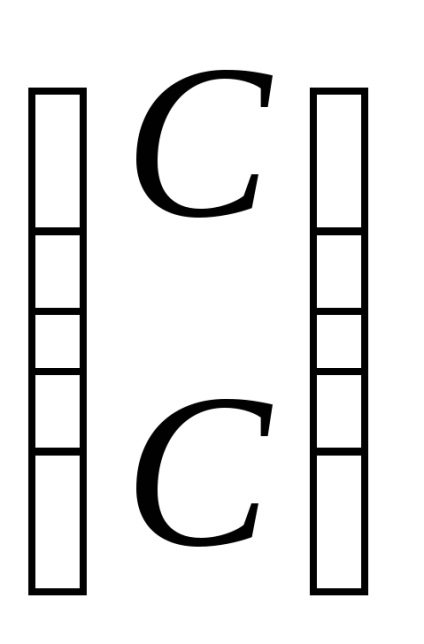
Отговор. собствена стойност
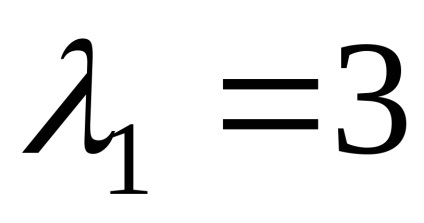
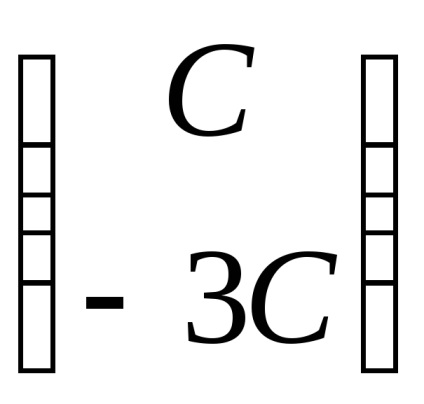
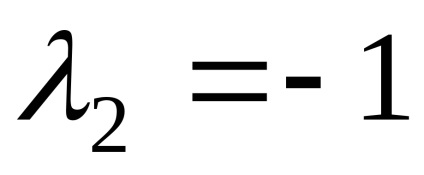
Пример 3. Намерете собствени стойности и собствени на оператор на линейна. в предварително определен основа matritseyA =
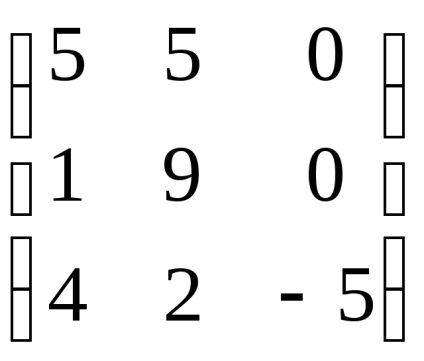
Ние намираме собствените стойности на линеен оператор. За да направите това, ние ще съставляват характерна уравнение и да намерят своите корени:
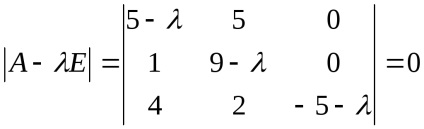
,
,
,
,
, ,
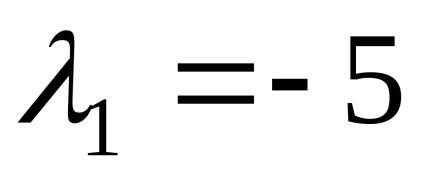
Ние намираме собствените вектори, отговарящи на собствената стойност
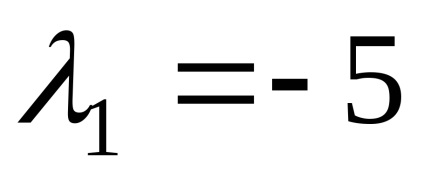
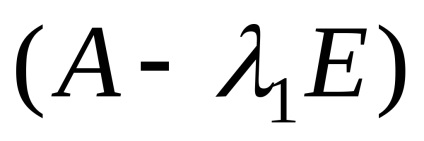
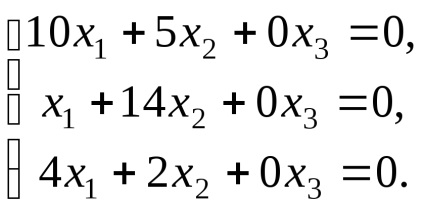

Тъй чин матрица система (R = 2) е по-малък от броя на неизвестни, системата има безкраен брой решения. Писане трансформира система и да го решите, получаваме
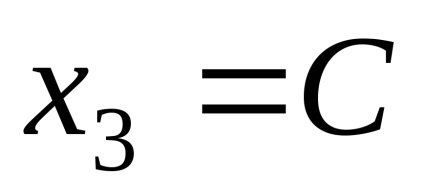
По този начин, собствени вектори, съответстващи на собствена стойност
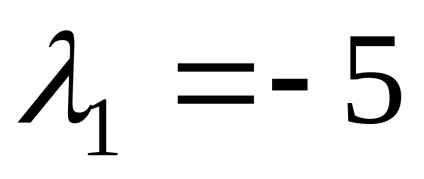
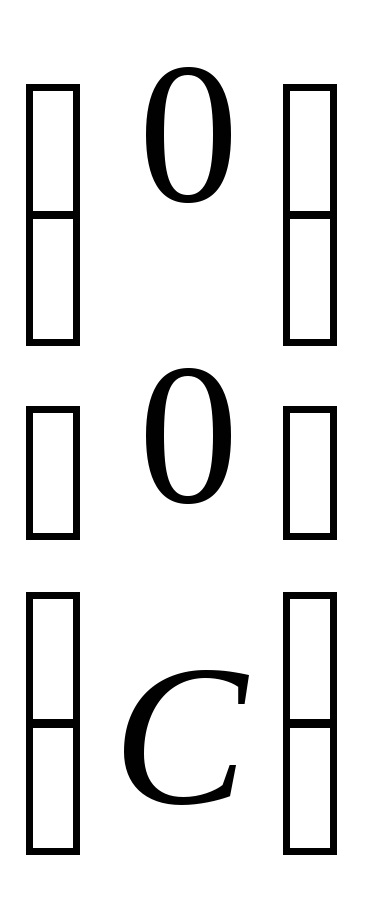
Ние намираме собствените вектори, отговарящи на собствената стойност
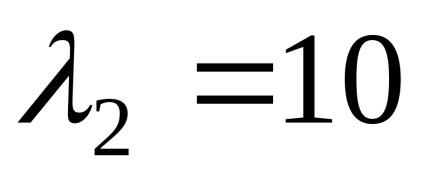
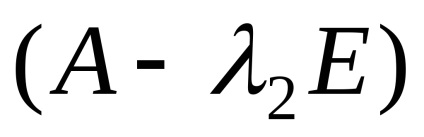
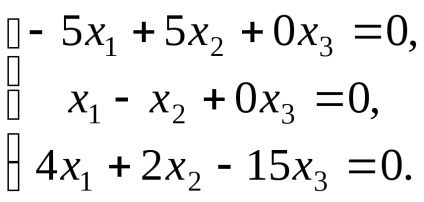
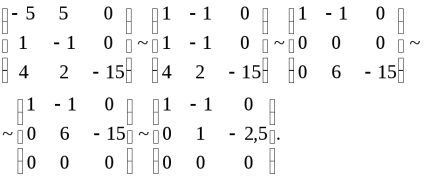
където системата е под формата
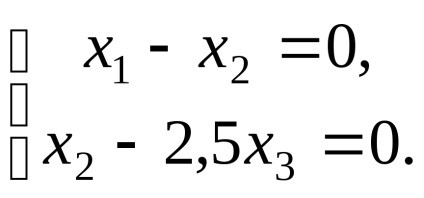
По този начин, собствени вектори, съответстващи на собствена стойност
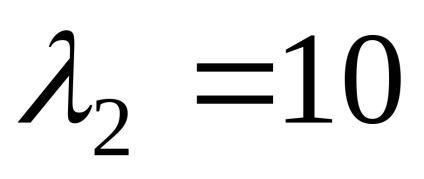
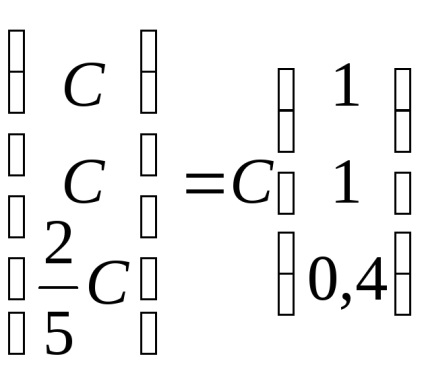
Ние намираме собствените вектори, отговарящи на собствената стойност
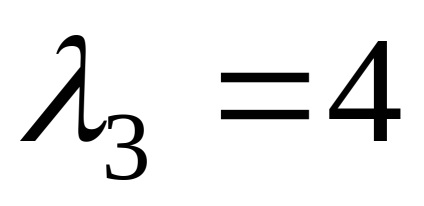
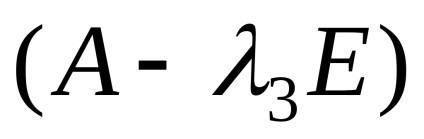
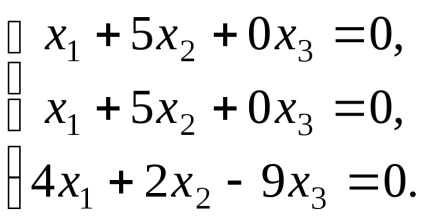
,
където системата е под формата
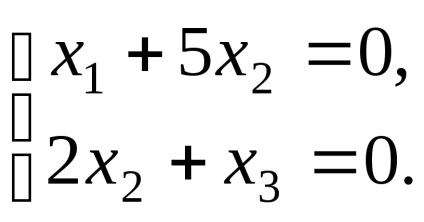
По този начин, собствени вектори, съответстващи на собствена стойност
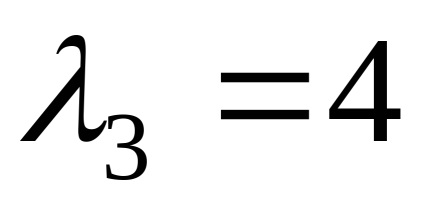
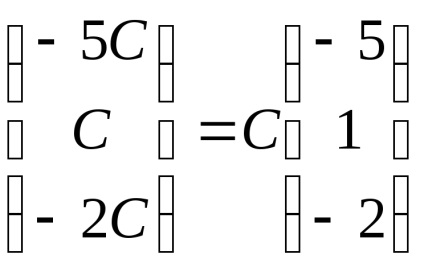
Свързани статии
