"Каналите. Краен функции. Основни понятия среща. В Шьонберг шлици "
Функции, подобни на това, което сега се нарича шлици са били известни на математици за дълго време, като се започне с най-малко Ойлер, но тяхното интензивно изучаване започна, всъщност, само в средата на ХХ век. През 1946 г., Isaac Шьонберг въвежда термина като наименование на класа на полином шпонки. До 1960, шлици са предимно теоретични изследователски инструмент, те често се появяват като разтвори на различни екстремни и вариационни проблеми, особено в теорията на приближение.
След 1960 г., с развитието на компютърните технологии започват да използват шлици в компютърната графика и моделиране, който продължава и до днес.
Съгласно шпонка (от английски шпонката -. Каишка, гребло) обикновено се разбира по части съвпада с функции опростена характер на всеки елемент от потребителите разделяне.
Класически една променлива шлицов конструира както следва: домейна е разделен на определен брой сегменти, всеки от които шлицов съвпада с някои алгебрични полином. Максималната степен на полином употребяван се нарича степента на шлицови. Разликата между степента на шпонката и гладкостта на получената дефект наречен шпонка. Например, има непрекъсната многоъгълна сплайн на степен 1 и дефект 1.
Каналите имат множество приложения в математическата теория, и в най-различни компютърни приложения. По-специално, каналите са на две променливи са силно използвани за определяне на повърхностите в различните системи за компютърна симулация.
1.1 криви Безие
Безие криви на Безие или Бърнстейн бяха разработени през 60-те години на ХХ век, независимо от Пиер Безие и Пол де Casteljau.
Криви за първи път са представени на обществеността през 1962 г. от френския инженер Пиер Безие, който ги е разработена независимо от де Casteljau, да ги използва, за да компютърно проектиране тяло на автомобили. Криви са наречени на името на Безие именно де Casteljau нарича рекурсивна начин за определяне тях разработена криви (де Casteljau алгоритъм).
Впоследствие това откритие се превърна в един от най-важните инструменти за компютърно проектиране и програми за компютърна графика.
Bezier крива - параметри крива дава с израза:
- позоваване характеризиращи вектори съставни пикове, и
, сближаване на първия си производно
.
Съществуването на такава централна теорема, както и още една серия от доказана теория Strang-Fix, по-специално наличието на функции задоволяване (2.7), дава алгоритъм за изграждане на основните функции на компактен подкрепа с необходимото сближаване свойства.
3. В-шпонки Шьонберг
Числените математика наречени B-сплайн сплайн функция като най-ниската носител за дадена степен, гладкост и за разлагане домейн. Основният теорема гласи, че всяко сплайн функция на определена степен, гладкост и домейн може да бъде представена като линейна комбинация на В-шпонки и съща степен на гладкост на същия домейн. [1] Терминът B-сплайн се въвежда J. Шьонберг и свиване на фразата "база шлицов". [2] В-шпонки може да бъде изчислена като се използва алгоритъм де грубиян, като резистентност.
В CAD системи и компютърна графика Терминът B-сплайн често описва кривата на шпонка, която се определя от сплайн функции, изразена от линейни комбинации на В-шпонки.
Когато единиците са на еднакво разстояние една от друга, казват те, че B-сплайн е еднаква, в противен случай той се нарича нехомогенни.
Когато броят на възли съвпада със степента на шлицови, B-сплайн крива на Безие дегенерира. То представлява най-основната функция определя от местоположението на възли. Мащабиране или паралелно транспорт на база вектор не се отразява на основната функция.
Spline, съдържаща се в изпъкналата обвивка на нейните контролни точки.
Основна сплайн на наш степен:
.
Тя не изчезне само за интервал [Ti, Ti + N + 1], т.е. .:
С други думи, промяната в една контролна точка се отразява само на местния поведението на кривата, а не на глобално, като в случай на криви на Безие.
основа функция може да бъде получена от Bernstein полином
B-сплайн и някои от най-често използваните бази
Теорема Strang-Fix показва, че ако стандартен краен функция
избрани въз основа на състоянието (2.7), след това (2.4), конструиран на базата на неговите преводи, ще притежават добро приближение свойства.
Шьонберг предлагат интересен клас функции задоволяване (2.7). функция
наречен B-сплайн (Шьонберг) степен
, ако нейната трансформация на Фурие, даден от
Както можете да видите, функцията (6.8) отговаря на всички условия (6.7).
Основа на стъпки
Доста лесно да се покаже, че за
Той представлява сближаване на непрекъсната права линия с прекъсната производни. в размер на приближение
Той има втори ред, в размер
- на първо място. Това приближение най-често се използва за решаване на диференциални уравнения на втория метод за проекция. Това води до най-простите формулите за интегралите и най-рядко матрица за неговото изчисляване.
В допълнение, тази основа, тъй като р = 1, има една функция - за апроксимираната функцията
съвпадат със стойностите на функцията на точки на мрежата
, който ви позволява да намерите бързо начално приближение за
.
Това е по части кубичен сплайн полином, който се получава чрез намотка:
.
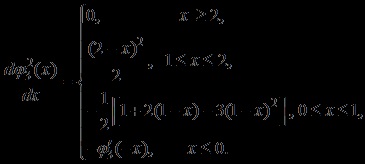
Формат на печатните носители
увеличи до четири (
). Имайте предвид, че, за да се гарантира приемственост в точките на втората производна
. Както вече споменахме, за сближаване на нормата
четвърти ред, в размер на
5. J. Alberg Nilson J. Walsh - .. Теорията на шпонки и техните приложения
Свързани статии
