373. Четири от монетата. Вземете 4 еднакви монети и ги поставете на масата без помощта на други монети или други помощни средства, така че петата монетата може да бъде точно за добре до данните, без да се движат четири последния (показан сенчести кръга представлява петата монетата).

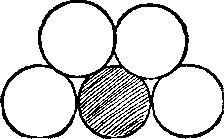
Разчита само на собствените си здраво око, най-вероятно ще се провали. В същото време, състоянието може да се извърши с абсолютна точност. Но как?

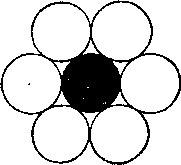
374. Шест монети. Място 6 от една и съща монета на масата, а след това ги поставете, както е показано с бели кръгове, така че понижава седми монетата (черен кръг) в центъра, щеше да я доведе по този начин в контакт с всичките шест монети. Вие искате да се кандидатира за сигурност, а не "на око". Повишаване на всяка монета от масата (в противен случай не би получил никакви загадки) или да извършва измервания не са разрешени. На Ваше разположение са само на шест монети.

Комбинаторните и топологични проблеми

375. Грешен магически квадрат. Поставени тук в дясната фигура показва магически квадрат, съставен от номера 1-16 включително. Сборът от числата във всеки ред, всяка колона и всеки от двата големи диагонали е равен на 34. Сега да приемем, че не ви е позволено да се използват цифрите 2 и 15, но вместо това можете да възпроизвеждате всякакви две числа вече използвани преди това.

Как да се организира номерата за новия площад на сумата от всички редове, колони и диагонали да остане равна на 34? Успехът зависи от това, което номера смените 2 и 15.

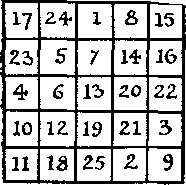
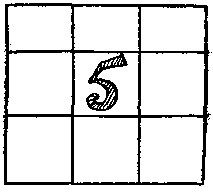
376. недоразумението с магия площада. Ето един магически квадрат на петия ред. Аз открих, че по-голямата част от хората не са запознати с теорията на дълбоки магически квадрати, убеден, сякаш в петия ред площади в центъра на номер 13. Един читател трябва задължително да престои в продължение на много години, развеселен от този квадрат, бях изумен, когато той научил от мен че в центъра на площада може да бъде всяко число от 1 до 25.

Докажете, че това е вярно. Опитайте се, например, направи магически квадрат на петия ред, в центъра на която е трябвало да 1.

377. Разлика квадрати. Можете ли да поставите 9 числа в квадрат, така че във всеки ред, всяка колона и във всеки един от разликата в големи диагонали между сбора от двете числа, а трети цифри са съчетани помежду си? На тази фигура е показана квадрат, при което всички редове и колони се удовлетворяват изисква условие - разликата в тях е 3 (например, 4 + 2 - 3, 1 + 9-7 6 + 5 - .. 8, и т.н.), но диагонал "изпомпва" поради разликата 8 - (4 + 1) и 6 - (1 + 2), получен забранен начин не един на фигурите следва да се приспадне сумата от другите две, и сумата от 2-1.

Колко решения съществуват?

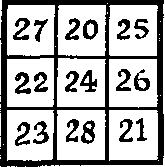
378. Не се прави нищо? Ето един прост магически квадрат, сумата от кои номера на всеки ред, във всяка колона, върху основните диагоналите са равни на 72. пъзела е да го превърне в мултипликативна магически квадрат, чийто продукт номера във всеки бар, във всяка колона, или на който и да е от големите диагонали, ще съвпадне с друг. Не е позволено да се промени всеки брой места, или да добавите към тях е нещо, нито дори да използвате всички аритметични знаци! Можете да преместите само цифри вътре една клетка. Така че, вместо 27 е позволено да вземат 72.

Ако успеете да вземете "ключът" към разтвора, проблемът ще бъде изключително проста. В противен случай решите пъзела е почти невъзможно.

Напълнете квадрати (вж. Фигура) номера (във всеки случай различен, така че няма две клетки не съдържат същите фигурите), така че сумата от номерата е възможно в по-голям брой колони и редове върху диагоналите, равно на 15. По време на следа "секреция "фокус бе назначен за голямата награда, но за да получите най-правилното решение не е възможно да се никого.

Може би на читателя, за да разбера какво става?

380. магически квадрат от четири цифри. Тъй като този квадрат се състои от една и съща дата от 1234, разбира се, че сборът от числата във всички редове, колони и диагонали са равни. Същността на пъзела е да се създаде и да публикувате 9 различни четирицифрени числа (състоящ се от един и същ четирицифрен номер), така че те също образуват правилен магически квадрат. Имайте предвид, че всички номера трябва заедно съдържат девет копия на всяка от цифрите 1, 2, 3, 4, и че това трябва да бъде истински четири двуцифрени числа без фракции; Без номера тук не са разрешени.

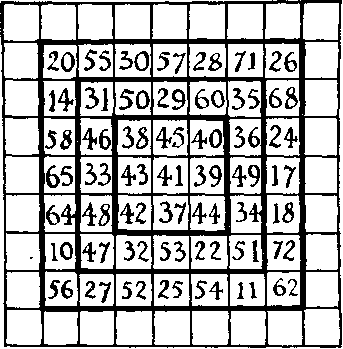
381. Прогресивни квадрати. Ето един магически квадрат, което е постоянна величина, т.е. сумата от числата във всеки ред, всяка колона и всеки от двата диагонала е равен на 287. Ако премахнем с броя, разположени в краищата, той ще бъде още един магически квадрат константа е равно на 205. Ако ние отново се премахнат екстремни номера, можете да получите на площада с постоянен 123. Сега Попълнете празните клетки с номера 1-83 включително, така че да се получи магически квадрат с постоянен 369 да е от своите 20 линии.

382. Условно магически квадрат. Въпреки сравнително проста конструкция на магически квадрати какво да добавя, но на самия обект там е много обширна, макар и разпокъсана, литература, леки вариации с някои нови условия винаги предизвикват интерес. Това не е трудно един пример.

Може ли да се изгради магически квадрат, чийто сбор на числата във всеки ред, всяка колона и върху всяка от двете големи диагонали, щеше да е същото, на числата от 1 до 25 включително, ако се поставят в сенчестите клетките само нечетни числа, а други дори? Има много решения на този проблем. Можете ли да намерите най-малко един от тях?

383. В петолъчна звезда. Пъзел със звездите имат особена притегателна сила. Аз ще дам един пример за пъзел, с една проста петолъчка.

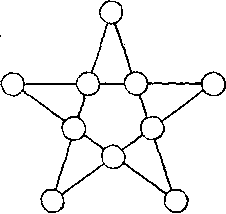
Във всеки кръг петолъчка показано тук трябва да поставите различни номера, така че сборът от всички четири числа на една и съща права линия, равен на 24. Решения с десет последователни числа не съществуват, но можете да използвате всеки от цели числа, които искате.

384. шестолъчна звезда. В предишната задача, ние счита случая на петолъчна звезда. Оказва се, че с шестолъчна звезда е така дори и по-интересно. В този случай (вж. Фигура), винаги може да се използва последователните номера 12 1-12 и сумата на четирите номера на всеки ред винаги ще бъде равен на 26. Сумата на номерата в шестте върхове може да бъде всеки брой 24-54 включително с изключение на 28 и 50. в този пример, тази сума е равна на 24. Ако вместо всяка от числата, които ще се замести с разликата между него и 13, ще получите друго решение, освен това на този, сумата от върха, равен на 54 (78 минус 24). Две допълнителни суми в съвкупното винаги дават 78.