Паралелното ИЗЯВЛЕНИЯТА многоцифрени числа на модулна структура на данните на

1 Медицински университет "Сургут държавен университет"

Документът описва паралелно извършване представителства на супер-голям брой многобитови използващи остатъчен класове система (CRS), китайският Остатък теорема (CTO) и малко теорема на Ферма. Такава мулти-битово представяне на числата дава предимства по отношение на времето за изчисляване операции в много по-голям обем от данни, които се обработват, както всички обработка на информация се извършва паралелно и независимо. Паралелно оглед позволява показване на милион или повече цифрени числа и може да се използва широко в кодирането на информация в ултрабързи компютърни алгоритми и тестване на суперкомпютри. Въпреки някои недостатъци, които от своя страна могат да бъдат преодолени, модулна система или система за остатъчни класове е уникален математически среда за паралелни изчисления. Ето защо, тази система може да бъде взето под внимание при проектирането на системи с висока производителност на базата на програмируеми логически интегрални схеми (FPGA) и многоядрени процесори.

Китайски остатък теорема

малко теорема на Ферма

остатъчни класове система

1. Amerbaev VM Теоретичните основи на компютърната аритметика. - Алма Ата, Наука, 1976 - 320 стр.

2. Buchstab AA теория на числата. - М. Science, 1975.

3. Василенко ON Съвременни методи за изпитване primality // Cybernetic събиране. Нова серия. - 1988 - Vol. 25. - стр 162-187.

В днешния алгоритмичен теория на големите и много големите числа да играе важна роля в криптографията за изграждане на шифри с различна сложност, както и да се провери изпълнението на суперкомпютри [4, 8]. Изследване на много големи числа [5] показва, че те имат стойности, които са трудно или почти невъзможно да си представим малко по малко в конвенционалните позиционни номера системи.

Ако номер 22147483647 = вдигна специфичната мощност, тя ще има повече от един милион бита. Следователно един такъв номер е неуместно да се обобщи, позиционна бройна система в реално първоначалното състояние.

Представлява изключително големи многобитови номера, използвайки конвенционална позиционна система номер, под формата на информационната система е показано на Схема изчисляване ultralarge номера (фиг. 1), и ги анализира.

Диаграмата показва, че на входа на номерата на ultralarge изчисление алгоритъм (ляво стрелки) са изключително големи многобитови номера, стрели "отгоре-надолу" означават позиционна бройна система и аритметични операции. На изхода на резултата от ultralarge алгоритъм-номер. Въпреки това, ако броят на резултати, за да се покаже в една нормална позиционна система, има проблеми:

1. Броят не се побира в стандартен компютър интервала [0. 231].
2. Времето, прекарано на представяне на числа в генерализирана позиционна система.
3. Натоварването на RAM, ако броят е съставена от свързани списъци.

В схема абстрахиране на много голям брой мулти-битов (фиг. 2), получен на изхода на броя на супер-голям, което не се вписва в един типичен компютър диапазон. Визуално извършва действие с този номер не е възможно, тъй като отнема стотици страници на файлове от всякакъв тип от операционната система Windows.

Във връзка с това много голям мулти-битови числа A = 22147483648 ефективно присъства в nonpositional корен - остатъчен класове система, в която не носене от по-ниските битове до по-висока.

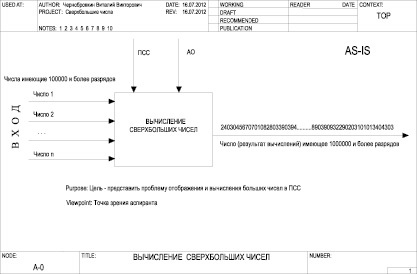
Фиг. 1. схема за изчисляване на броя Superlarge

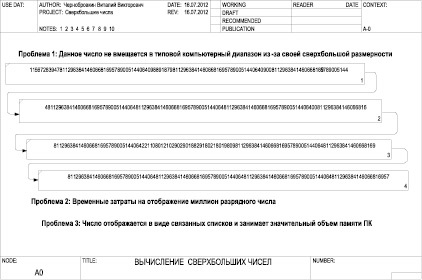
Фиг. 2. Схематично представяне на много голям абстрактно цифри във формата на свързани списъци

Съществува проблем, който е следното: ако супер-голям цифрено число, представено чрез система остатъчен класове [5, 7], броят на остатъци, както и избран система база ще бъде голяма, което от своя страна се отразява на изчислителни методи.

Представяме цифров диапазон в двоичен позиционна система [265537. 22147483648].

Приемане 1 А = номер 22147483648, с броя на битовете от интервала [265537. 22147483648] или повече, това може да се нарече допълнително високо число.

Номер като един милион или повече бита може да се нарече много големи мулти-малко, тъй като има голяма числена стойност в реално изпълнение.

Приемане 2 Superlarge многобитови числа, представени в остатъчната система класове зависят от теглото на позиционен ранг | Z | P [1], и по този начин могат да се състоят от голям множество избрани модули и остатъци, съответно. Тегло позиционен ранг | Z | P зависи от съдържанието на броя на простите числа. При изчисляването на много големи номера на остатъчни класове система е необходимо да се разгледа по следната формула:

където А - изчисление номер резултат; - на базата на модулната система са относително прости.

номер Приемане 3 ultralarge може да бъде представена от системата за остатъчен клас под формата на остатъци от остатък [3, 5, 6, 7]

на ≡ б (мод п). (2)

Възможността за такова изобразяване на брой се определя от следните теореми.

Теорема 1 (китайски Остатък теорема) [2, 3, 5, 6, 7].

Всяко положително цяло число в остатъчната система класове могат да бъдат представени като набор от остатъци (от остатък), като се раздели броя на (модули) система избрана база.

Доказателство: Нека A = номер 22147483648 представена в системата като остатъчна класове

където А1, А2, ..., един - малките неотрицателни остатъци (остатъци), образувани от число разделяне на А за избрания основата

където пи - са сравнително премиер.

Ако представяне на броя (3) е снабдена само

Тогава броят на А е, както следва:

А ≡ а1 (мод p1);

А ≡ а2 (мод p2); (7)

А ≡ на (мод PN).

Теорема 2 Ако редица пи = Р1, Р2. PN са сравнително премиер, а след това за всеки остатъци А1, А2. на, така че 0 ≤ на ≤ PN, за всички I = 1, 2. п съществува редица А, който когато е разделен от пи добиви остатък AI за всички I = 1, 2. п

Доказателство: Ние използваме индукция нататък. За п = 1 твърдението, е очевидна. Да предположим, че теоремата е валидна за п = к - 1, т.е. съществува номер М, давайки остатък, когато ри разделен НС пи защото ∈. означаваме

г = А1, А2. ак-1. (8)

Разглеждане на номера М, М + г, М + 2d. M (ак - 1) г. Ние показваме, че поне един от тези номера дава останалата част, като разделено на RK ак. Да приемем, че това не е така. Тъй като количеството на номера равна AK, и възможни остатъци могат да бъдат не повече от ак чрез разделяне тези номера в ак - 1 (тъй като никой от цифрите не дава RK остатък), след това има две числа, имащи еднакви остатъци между тях. Нека този брой

М + М + TDM SDI за 0 ≤ S ≤ ак

и 0 ≤ т ≤ ак и S ≠ т. (9)

Тяхната разлика

(М + SD) - (М + TD) = (S - т) г

Той е разделен на АК, което е невъзможно, тъй като 0 <s – t 

Тъй като ние говорим за милион цифрено число, а след това се опише истинските проблеми на изграждането им в системата на остатъчна клас:

• Избор на броя на бази
• Bit избран бази
• многобитови остатъци

Това означава, че ако ние се изгради изключително голям брой, които имат един милион или повече цифри, броят на бази система ще зависи от дълбочината на битовете от тези номера. Например, ако думата дължина на всяка от избрания малката основа, съответно, количеството на основата трябва да се увеличи. И обратното, ако избрания малко голяма причина, те трябва да се намали до необходимия брой. Ние говорим за разширяване или свиване на базата на системата на остатъчни класове [7]. Друг проблем е, че при показване на много голям брой A = 22147483648 в остатъчни класове система остатъци могат да бъдат и много малко.

Като цяло, по-горе проблеми могат да бъдат решени с помощта на малко теорема на Ферма, чиято доказателство е дадено в [2, 6] и китайски Остатък теорема [2, 3, 5, 6, 7].

Основният смисъл на малко теорема на Ферма е, че ако р - положително просто число, а - цяло число, а след това

АР-1 ≡ 1 (мод п), ако р - просто число (10)

Това означава, ак ≡ ар (мод п) и направи достатъчно изчисления само за експоненциално, скоростта на които е по-малко от р - 1.

С помощта на китайски остатък теорема, ние можем да се опрости дисплея много големи числа. Показване на тях като мощност остатък по модул н, ако знаем разцвета на множители. Да приемем, че всеки основен фактор в тази експанзия идва с кратност 1, тъй като в този случай методът е най-ефективен.

Да приемем, че разширяването има формата

където 0

За числа с и м първи намерите AM приспадане за всеки модул пи. Ако простите делители не е твърде голям, а след това при изчисляването ще бъде много бързо, дори и за голяма м и, защото тя ни помага да направим Малка теорема на Ферма (стр. 10).

Ако приемем, че изчисленията се правят и

ч ≡ r1 (мод P1) и 0 ≤ ≤ r1 P1;

ч ≡ r2 (мод p2) и 0 ≤ r2 ≤ p2; (12)

ч ≡ RK (мод п.к.) и 0 ≤ ≤ RK пк.

Ето защо, за да се определи приспадане ч по модул на п трябва да реши системата на сравнения:

Спомнете си, че модулите на системата - различен двойки относително прости числа. Следователно, от китайски остатък теоремата, системата винаги има решение, например R, 0 ≤ ри ≤ пи - 1. Освен това, всеки два от тези решения са еднакви модул p1. п.к. = п .... Тъй като съм също е решение на системата, ние имаме ч ≡ R (мод н). Следователно, г - ampo остатък модул п.

Пример. Surjectively показва броя 22147483648 А = остатък избран бази p1 = 11, Р2 = 13, P3 = 17, Р4 = 19. Чрез промяна на степента на споменатите единични номера 2147483648-1 = малко теорема 2147483647 Ферма е приложимо, за които намират остатъци модул степен 2147483647 (за Р1) на всяка избрана базова Р1, Р2, Р3, Р4. след това

пи-1 = 11-1 = 10; пи-2 = 13-1 = 12;

пи-3 = 17-1 = 16; пи-4 = 19-1 = 18; (14)

a'1 = 2147483647 = 10 мод 7;

a'2 = 2147483647 = 12 мод 7; (15)

a'3 = 2147483647 мод 16 = 15;

a'4 = 2147483647 мод 18 = 1.

22147483647 А1 ≡ = 27 (мод 11);

а2 = 22147483647 ≡ 27 (мод 13); (16)

а3 = 22147483647 ≡ 215 (мод 17);

≡ 22147483647 А4 = 21 (мод 19).

Накрая, броят на A = 22147483647 ще изглежда така:

27 ≡ 7 (мод 11);

27 ≡ 11 (мод 13); (17)

215 ≡ 9 (мод 17);

2 ≡ 2 (мод 19).

1. паралелизация представяния ultralarge многобитови номера използват остатъчен класове система има предимството, че времето за изчисления с голямо количество данни, за да бъдат обработени, както се случва обработка всички данни паралелно и независимо.

2. Всяко цифрено число може да бъде представен под формата на остатъци от електроцентрали остатъци.

3. Над номера представени в паралелен начин може да се осъществи ускорено паралелни изчисления.

4. Ако образуването а.с. остатъци, получени независимо, всяко изчисление ще възникне независимо един от друг.

Inyutin SA DTS Професор по "Проектиране на компютърни системи", VPO "Руския държавен технологичен университет. KE Циолковски (МАТИ) ", Москва;

Baharev MS DTS Професор по "Нефт и газ Бизнес" VPO "Сургут на нефт и газ институт, Тюмен-членка на нефт и газ университет клон" Сургут;

Krishtop VV Проф професор, ръководител на "Физика", далекоизточен държавен университет транспорта, Хабаровск, професор в Kwangwoon университет University, Корея.

Ние Ви донесе списания, издавани от издателство "Академията за естествени науки"

(High импакт фактор RISC, списания теми, обхващащи всички области на науката)

Научно списание | ISSN 1812-7339 | PI №77-63397

Технология бюро за помощ - [email protected]

Изпълнителният секретар на списание Bizenkova MN - [email protected]

съдържание Magazine е достъпно на Creative Commons «Attribution» лиценз ( "Признание") 4.0 World.

Свързани статии

• Сравнение на многоцифрени числа