Това означава, че безкрайно множество А и Б са равностойни, AB. Те имат "една и съща мощност." Интересно е, че това е еквивалентно на неговото mnozhestvoA podmnozhestvuB, A
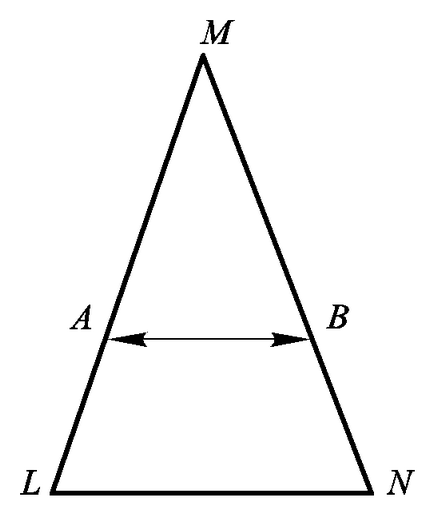
Фиг. 7.6. Създаването на едно едно съответствие между равни страни на равнобедрен триъгълник.
2. PustLM iNM- равни страни на равнобедрен treugolnikaLMN (фиг. 7.6).
Свързване страни точки А и В на триъгълник равни сегменти от прави линии паралелно osnovaniyuLN. Ние се получи едно към едно съответствие между точките на комплекта определени otrezkamiLM INM. Следователно, тези комплекти са еквивалентни и имат една и съща мощност.
3. Сега нека LN и MN - (. Фигура 7.7) LMN неравни страни на триъгълник. Свързване на точките А и В от двете страни на правите сегменти успоредна на страничната LM. Ние се получи, че неравностойно между множество партии се определят точки с еднаква сила. въпросът
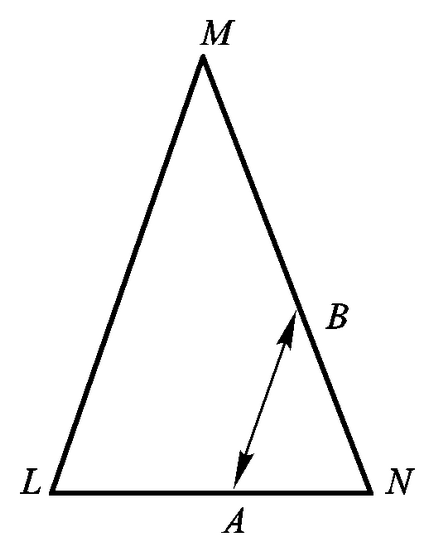
Фиг. 7.7. Създаването на едно едно съответствие между неравностойни страни на равнобедрен триъгълник.
че storonyLN IMN да има различна дължина, но всеки един от тях включва безкраен набор от точки, които са също толкова "много".
изброимо множество
Комплектът се нарича изброимо. ако това е еквивалентно на множеството на естествените числа.
По този начин, възможността за "преномерират" всички елементи на комплекта определя броими. Тази задача не е винаги лесно решен.
Трябва да отбележим някои свойства на изброимо множество.
1. От всеки безкраен набор винаги може да изберете изброимо множество.
В действителност, ако А е безкрайна, а след това можем да изградим изброимо mnozhestvoN следва. Изолира се като първият елемент mnozhestvaN например elementmnozhestvaA .tak KaKa безкрайна, след изключването на тях elementasohranit си безкрайност. Освен това, отделно от останалата множеството елемент закрепване към множество Н. след това от безкраен брой отделим елемент поставяне egokN, и така нататък. MnozhestvoN става: ще преброим.
Дайте пример за онагледяване този имот.
2. Всеки безкраен набор от изброимо множество е броим.
Ако зададете е броим и B- безкрайно подмножество, а след това последователно сортиране на елементите на А. ние ще се срещне с елементите на серия Б и ги номериране, че има елементи на набор Б. B

3. Съюзът на който и да е краен или изброимо множество изброимо множество е изброимо множество.
За да докаже това, нека разгледаме свойствата на изброимо множество:
Ние формират тези набори нов набор от
Тя се формира така, че се намира на първия елемент, последвано от елементите на което сумата от индексите ravna3. potom4. и така нататък. Такъв пакет включва всички елементи на снимачната площадка се е броим, ekvivalentnymN.
кардиналност на континуума
Като се има предвид свойствата на изброимо множество, ние се опитахме да докажем countability на определени определя безкраен. Въпреки това, дали всички определя безкраен са броими? За да откриете безброй комплекти, трябваше да преодолее много трудности. И Б. Болцано и Cantor, чувствайки, че идеята за създаване на кореспонденция едно към едно е ключът към намирането на силата на безкрайните множества бяха близо до решаване на проблема в същото време. Б. Болцано идва за първи път метода на оценка на безкрайни серии от създаване на кореспонденция едно към едно, както и първата, Cantor е успял да намери безброй. Той е безкраен и не е еквивалентно на множеството на естествените числа.
Теорема. Линията на сегмент брой съдържа безброй точки.
(Друг начин да се докаже тази теорема ", диагонал метод на Кантор" е показан в приложението)
Да приемем, напротив: - изброимо множество точки. Нека да ги изброявам:
Има ли някой от тази точка на отсечката е включена в тази последователност?
За да се докаже теоремата за намиране на точка от отсечката, която не се покрива от тази последователност.
За тази цел, се разделят на сегмент на три равни части (фиг. 7.8). Ние получи сегмента:
Фиг. 7.8. Изграждане на точки не са включени в поредицата.
Защо ни разделят на 3 части, а не на половина или на 4 парчета? Защо са тези три части трябва да са равни?
Най-малко един от тях не е най-важното. Изберете мястото, разделете новия сегмент е подмножество на интервала, отново на три равни части и изберете този, в който не съществува точка (в този "трети" няма да има точки, а точките, както е посочено по-горе). На следващо място, нов сегмент отново се разделят на три равни части и изберете тези, при които няма tochkia3 (както е показано на Ина точки няма да е), и така нататък. В резултат на това nan- ия етап ние получаваме един сегмент с дължина, която също все още няма точки ,,, .. Продължавайки този процес за неопределено време, ние откриваме tochkua. който не е включен в последователността
Действително, обща точка на тези сегменти. Като точка на сегмента, тя трябва да бъде включена в поредицата, но това е невъзможно, защото без значение какво ние се п, AN точка не може да принадлежи към съответния сегмент, както и буква а ще принадлежи на него, следователно, и е различен от всички АН. което доказва теоремата.
Мощност определя равностоен сегмент, nazovemMOSchNOSTYu континуум и обозначени bukvoyc.
Ние говорим за някои от тези комплекти.
Помислете за сегмента. Записите формула под
,
установява едно към едно съответствие между множеството и на снимачната площадка. Следователно, има има кардиналност на континуум.
В допълнение, множество от:
Те имат една и съща мощност на континуум век. тъй като тя се различава от снимачната площадка на определен брой точки, които ги държи властта.
А напълно неочакван резултат е получен чрез Cantor, първоначално се приема, че квадрат със страна, равна на 1. Тя съдържа "повече" от интервала пиксел. Те са еквивалентни.
"Мога да го видя, но не го вярвам," - пише той в писмо до Дедекинд.
В действителност, ако подредени в квадратен система koordinatXOY. както е посочено по-долу Нарис. 7.9. след това всички от вътрешното си tochkeW. като координати
Той може да бъде свързан с точка на интервала:
Различни точки на W квадратен ще съответстват на различни точки на интервала. Може да се покаже (с помощта на по-стриктен аргументи), че тази кореспонденция е едно към един-към-едно, толкова много точки на площада със странична ravnoy1. и един сегмент има същата мощност. Освен това, не само квадратна, но, например, един куб или сфера, съдържа "същия брой" точки, колко от тях съдържа сегмент.
Сравнение на множеството на естествените числа е броим и неизброимо множество от точки в този сегмент е въпросът дали наборът от междинния мощност на разположение? С други думи, не е безкраен набор, в които броят на елементите "повече" от естествени числа, а "по-малко" от точките в този сегмент? Това е znamenitayaproblemaKONTINUUMA. която все още е от значение за много математиците. В началото на шейсетте години
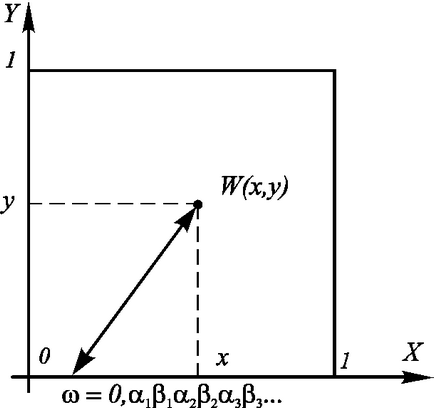
Фиг. 7.9. Един кореспонденция между точки в квадрат слот и точки.
Двадесети век, бе установено, че има като система от аксиоми, в която континуум хипотеза е вярна, и аксиоматична строителството, в която тя е фалшива.
Следното твърдение е доказано в теорията на множествата:
За всеки набор А, има много висока мощност (вж. 2 и 3).
Задава най-голямата сила е налице. (Виж 3).
Наборът от всички подгрупи на зададете е с капацитет по-голям от moschnostA.
Множеството от всички подгрупи на групата има изброимо кардиналност на континуум.
Задайте теория е пълен с предизвикателства и парадокси. и че в момента са от интерес за изследователите. Един ofthem обсъдено по-горе. Тук представяме klassicheskiyparadoks Ръсел.
Нека M - комплект от всички множества, и N - множеството от всички негови подгрупи. Тогава mnozhestvaN власт всички подгрупи трябва да бъде по-голяма мощност mnozhestvaM (според 3). Но opredeleniyuN - подгрупа, следователно, N = М. Получаваме фатално противоречие.
Свързани статии
