Неравенството на аритметика и геометрична (Cauchy)
Средноаритметичната стойност на п положителни числа е не по-малко от геометрична стойност.
освен това, равенство се постига единствено и само ако
Специален случай на това неравенство, свързваща средното аритметично и средното геометрично на две положителни числа, известни още от древността. Най-често това е доказано с помощта на геометрична интерпретация.
Ние изграждане на кръг с диаметър AB = а + б.
От произволна точка С на диаметъра на кръга ще проведе CD перпендикулярно.
Чрез имот правоъгълен триъгълник, височина, проведено от хипотенузата. е средна геометрична между издатините на краката на хипотенузата:
Присъединяване точка С центриран кръг точка О. CO - радиус, така че е равен на половината от диаметъра:
т.е. дължина CO е средната аритметична стойност на а и б.
В правоъгълен триъгълник COD CD - крака, CO - хипотенуза.
Както хипотенузата е винаги по-голяма от крака. CO> CD, следователно, средната аритметична стойност на А и Б по-голяма от тяхната средна геометрична.
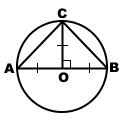
Ако AO = BO, т.е. = б.
(Тъй като> 0), и Q и този случай средната аритметична стойност на А и В е равен на средната геометрична стойност на тях.
Така, средната аритметична стойност на положителни числа а и б е не по-малко от геометрична стойност.
QED.
Като цяло, неравенството е доказано от Cauchy.
Свързани статии
