В метод LU-факторизиране (тази схема се нарича компактен схема Гаус ") разтвор на системата следната последователност от действия.
Матрицата е представен като продукт
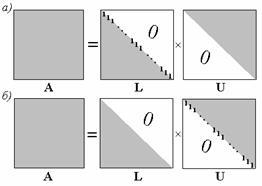
Фиг. 2.3. Структурата на матрици L и U в разширения Doolittle (а) и Крот (б)
където L - долната триъгълна матрица, U - горна триъгълна матрица. Това разлагане е уникален с предварителното избор на една от диагоналните елементи на матриците. В този случай, броят на елементите в матрицата съвпада с общия брой на неизвестните елементи на матрици L и U. Ако устройството се получи диагоналната L, такава разлагане се нарича разлагане Doolittle Ако устройството диагонал U (фигура 2.3, а.) - разлагане Крот (фигура 2.3. , б). В бъдеще, LU- множители на метод строителство ще включва разширяване на Крот.
Системата заменена от система
лесно решен в два етапа:
Етап 1. Като се има предвид триъгълна матрица L. лесно видим, че алгоритъмът Крот
Етап 2. Решението на тази система в алгоритъм шваба:
Общите разходи за прилагане на двете стъпки, когато N >> 1 правят дълги операции.
Връзки за изчисляване на елементи на матрици L и U в Крот алгоритъм. За тази размножават матрици L и U и равнява резултат А. чрез умножаване на правило матрица
Да разгледаме елемент (фиг. 2,4), разположени върху централната диагонал или долната триъгълна част на матрица А. За такова elementai ≥ й. От фигурата следва, че
Фиг. 2.4. Илюстрация на матрица изчислителни елемент разположени
под главния диагонал
тъй като аз ≥ й и. тук
Да разгледаме елемент (фиг. 2,5), разположен над главния
Фиг. 2.5. Илюстрация на матрица изчислителни елемент разположени
над главния диагонал
диагонална матрица A (за него й> и). В този случай,
Ние получени в резултат на съотношения, които позволяват да се изчисли елементите на матрици L и U. Последователността на изчисления: първата колона на матрицата се изчислява L. U. допълнително ред на матрицата и след това отново матрица L. колона допълнително ред на матрицата U на и т.н. (виж Фигура 2.6 .... който илюстрира диаграма на последователността изчислителни и съхранение матрици L и U).
Изчисляване колона на матрицата L и матрица U линия се нарича стъпка LU-разлагане. Тук, както например за съхранение на елементи на схемата на матрици А един, L, U след втората стъпка LU-разграждане (фиг. 2.7).
Броят на дълго аритметична операция в стъпка LU-разпадане, когато N >> 1 суми. решения Li- стъпка
линейни системи с триъгълни матрици -. Общият брой на операциите е приблизително равна на дългосрочните (както е в метода на Гаус)
Фиг. 2.6. Първоначалната матрица А (а), схема съхранение L и U матриците на (б), последователността на изчисляване на получените елементи за съхранение в схемата (в)
Фиг. 2.7 4'4 съхранение Схема елементи на матриците A, L, U след втората стъпка LU-факторизирането
.. Това означава, че основните разходи падат на LU-множители на А. Тази функция го прави особено привлекателен начин на LU-множители за решаване на линейни системи с една и съща матрица А. но различни страни с десен волан прави:
В този случай, разлагането на множители на матрица се извършва веднъж, изискващи дълги операции, както и всяка система решение със съответния дясната страна се реализира за подобни операции.
Изключително ефективно прилагане на метода на LU-факторизирането може да се получи, ако се ограничи класа на линейни системи с симетричен положителен определена матрица A. т. Е. Такова изпълнение се нарича по метода на Cholesky или от корен квадратен.
Предполагаме, че системата може да се реши
има положителен определен симетрична матрица А. В този случай матрицата е представена като
Тук - долна триъгълна матрица. Такова разширяване съществува и е уникален за положителни определени симетрични матрици.
Системата се превръща в
Векторът се търси чрез последователно решаване на две триъгълни системи с матрици:
За изчислените отношения матричните елементи считаме произволен елемент на матрицата:
Сумирането се извършва само да й. т. За. j≤i. Ние избираме член на стойност к = й:
Тези отношения ни позволяват да се изчисли колоните на елементите на матрицата.
Ефективността на този метод се постига в етап на разлагане на матрицата, т.е.. К. необходимо да се изчисли в този случай само матрицата. метод аритметични разходи Cholesky представляват дълги операции и операции за добив н корен квадратен.
Има и друг вариант разлагане симетричен положителен определена матрица, която избягва екстракция на квадратен корен операции. В този вариант се въвежда нова матрица чрез правилото
и - матрицата преди изчислява чрез схема Cholesky, - диагонална матрица с матрични елементи. Матрицата съществува и е по-ниска с триъгълна единица диагонал. В този случай,
Изчислената съотношението на матрицата елементи и може да се получи, както и преди, обикновено включваща матрица умножение
от което следва, че
т. к. единица диагонална матрица.
Такъв алгоритъм ще изисква два пъти броя на повторенията в схемата Cholesky. Въпреки това, ако ние се въведе промяната на променливите
изчисленото съотношение ще образуват
Има първо изчислява помощни стойности. и след това да ги използвате, за да се определят неизвестните количества и. Броят на повторенията такова подреждане алгоритъм на приблизително и съдържа квадрат операция екстракция корен.
Свързани статии
