Нека се върнем към модела на механичната система, както е описано в Пример 3.1. Уравнението на нелинейна модел
.
От втория ред уравнение може да отидете на автономната система на формата
,
Ако сега в системата за отстраняване на време Т, ние получаваме диференциално уравнение на траекториите на фаза равнина
ние можем да пренапишем последното уравнение, както следва:
След това, се предполага, че в и. след интегриране на уравнението в интервала до получаване на равенството
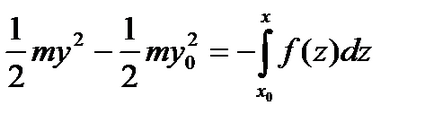
който може да бъде пренаписана, както следва:
Имайте предвид, че
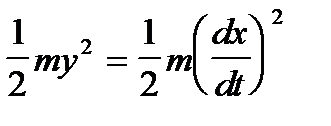
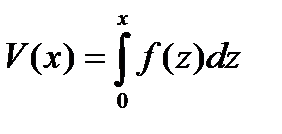
- формула е неговата потенциална енергия. По този начин, уравнението изразява закона за запазване на енергията:
където - общата енергия на системата.
Ясно е, че това уравнение - уравнение на траекториите фаза на нелинейни консервативна система, тъй като тя се получава чрез интегриране на уравнението
По този начин, различни стойности на фаза равнина Е съответстват на различни криви на постоянна енергия. Стационарни точки на системата са точки М * на (х *, 0), където Х * - корените. В този случай, ако пренапише на закона за запазване на енергията под формата на
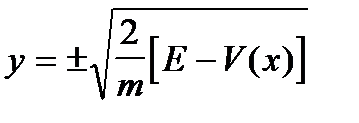
можете лесно да изгради фазови траектории.
Проведени общи съображения дават възможност да се разследва уравнението на движение на махалото в околната среда без никаква съпротива, която има формата
. където - положителна константа.
От уравнението е специален случай на уравнението. може да се тълкува като уравнение описва линейно движение на единица телесна маса без триене под действието на нелинейни пружини, при което възвратната сила е равна. В този случай, самостоятелна система, която съответства на уравнението, написана под формата
Singular точки тук ще са система от диференциални уравнения на фазови траектории ще приемат формата
Разделянето на променливите в крайното уравнение и интегриране, ние получаваме уравнението на траекториите на фаза
Последното уравнение е специален случай на закона за запазване на енергията, къде. и потенциалната енергия се изчислява по формулата
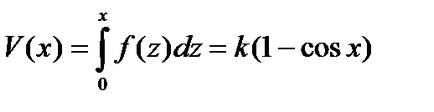
Определяне на стойността. можем да скица схематично изображение на поведението на траекториите на фаза равнина, ако се използва съотношението.
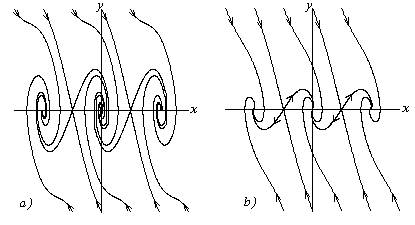
Получените фаза портрет показва (фиг. 3,3), че ако енергията се променя от преди. съответните фазови траекториите са затворени и уравнението има периодични решения. От друга страна, ако. съответните фазови траекториите не са затворени и уравнението периодични решения. Стойността в равнина фаза съответства на траекторията на фаза, която разделя двете различните видове движение, като траектория се нарича separatrix. Вълнообразните фаза траектории, лежащи извън separatrices съответстват на въртеливото движение на махало, и затворени пътища, разположени в зоните, ограничени от separatrices - му вибрационното движение.
Фиг. 3.3. Портретът фаза на нелинейни консервативна система
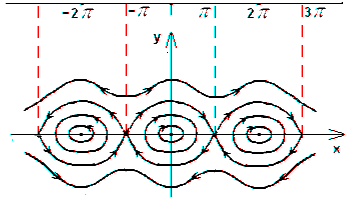
На Фигура 3.3 се вижда, че в квартала на фиксирани точки. където поведението на фазови траектории се различава от поведението на траекториите на фаза в квартала на фиксирани точки. където
Нека сега да видим какво ще повлияе на поведението на траекториите фаза на консервативна система на линеен триене. В този случай, уравнението става
Фиг. 3.4.Fazovye портрети консервативни системи с триене
Такава система ще бъде не-консервативни. Ако триенето е достатъчно малък, т.е. възможни колебания на махалото по отношение на положението на равновесие, може да се покаже, че траекториите фаза са показани схематично на фигура 3.4, а. Ако триенето предотвратява трептене на махалото по отношение на положението на равновесие, моделът на фаза траектории ще имат форма, показана на фиг. 3,4, б.
Ако сега се сравни фаза портрета на консервативни системи с последните две фазови портрети на не-консервативни системи, това може да се види, че траекториите затворените фаза в нисък коефициент на триене, се движеха в една спирала, и със силна триене - в пътя, който са част от единичните точки в определени посоки.
Фиг. 3.4.Fazovye портрети системи с триене: а - малка триене; б - високо триене