а) Комплексни числа представляват точки в равнината съгласно следното правило: а + BI = М (А; б) (фигура 1).
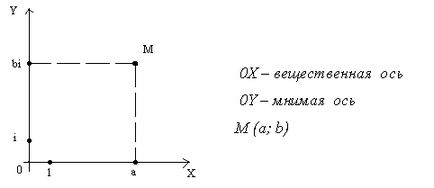
б) комплексно число може да бъде представена чрез вектор, който има начало в точка О и крайната точка в областта (Фиг.2).
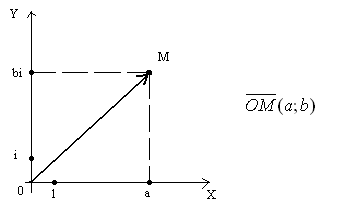
Пример 7 конструкт точки представляват комплексни числа: 1; - I; - 1 + I; 2 - 3i (Фигура 3).
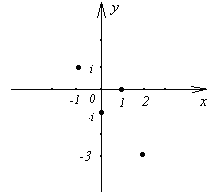
Тригонометрични запис на комплексни числа.
Сложна номер Z = а + би може да бъде настроен с използване на радиуса - вектор с координати (а, б) (фиг.4).
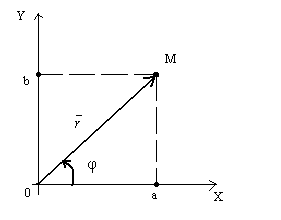
Определение. Дължината на вектора. изобразяваща комплексно число Z. Този модул се нарича и броя или определен R.
За всеки комплекс номер Z му модул г = | Z | Тя се определя еднозначно от ур.
Определение. Ъгълът между положителния реалната ос и вектора на посока. изобразяваща комплексно число, наречено аргумент на комплексно число, и Z означава Arg или # 966; ,
Аргумент на комплексно число г = 0 не е дефинирана. Аргумент на комплексно число Z ≠ 0 - multivalued стойност и се определя в рамките на срок 2πk (к = 0 - 1, 1 - 2, 2, ...): Arg Z = Arg Z + 2πk. където Z Arg - основната стойност на аргумента затворено в интервала (-π; π] т.е. -π. а = R · COS # 966;, б = R · грях # 966; , Следователно, комплексно число Z = а + би могат да бъдат написани като: Z = R · COS # 966; + I R · грях # 966; или Z = R · (COS # 966; + I грях # 966). Такъв запис на комплексно число се нарича тригонометрични форма на комплексно число. Пример 8. настояще в тригонометрични формата на комплексно число 1- аз.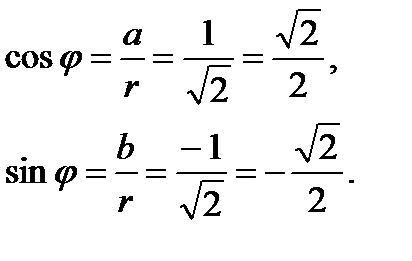
1 - аз = (COS + и син).
Свързани статии
