Дървени парчета 1

дефиниция

Wood парчета - структура на данни, който позволява да се извършват операции с много сегменти на масива за $ О (\ влизане N) $. Дървени части - универсална структура от данни, за които е възможно да се реализират неограничен набор от операции (понякога от голяма сложност: $ O (\ влезете ^ 2 N) $). Най-простият вариант на дължините на дървото Ви позволява да намерите на сумата или минималния интервал, и промяна на отделните елементи.

Изграждане на участъци от дърво

Дървени фигури - пълно двоично дърво, в което всеки връх е отговорен за един сегмент от масива. Коренът на дървото е отговорен за цялата решетка, нейните две дъщерни върхове - на две половини, и така нататък. На всеки възел, отговаря за участъка с дължина, по-голяма от $ 1 $, има две дъщерни върхове, съответстващи на Лявата и дясната половина на този интервал. листа на сегментите от дърво са отговорни за отделните елементи (сегменти с дължина 1 $ $).

Графично, това е, както следва (за масив от 8 елементи):

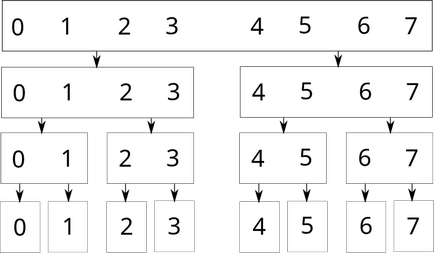
Всяка кутия - топ сегмента на дървото. Ако някой връх е отговорен за продължителността на странно дължина, след това един от своите подчинени, възли ще отговаря за един сегмент с дължина $ \ lceil \ rceil $, а другият - за дължината на отсечката $ \ lfloor \ rfloor $. Например, така че изглежда като дърво сегменти за масив от 13 елемента:

За масив от $ N $ парчета елементи от дърво има около $ 2 n $ върхове ($ н + + + \ ldots $), а височината му е от порядъка на $ \ дневник п $.

Основните сегменти на имота на дървото, на които са изградени всички алгоритми работят с него всеки непрекъснат сегмент в масива от $ N $ елементи можете да бъде представен от около $ 2 \ дневник п $ върха в сегмента на дърветата.

Например, сегмент [1 $; 11] Дължина на $ масив $ 13 $ могат да бъдат представени чрез следните върхове:

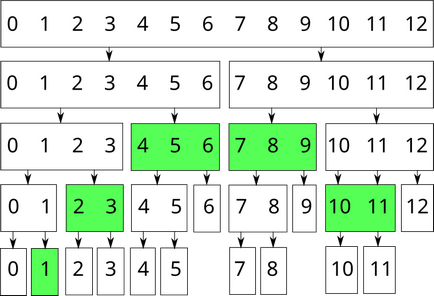
Дървени части за намиране на сумата

Един от най-простите функции, които могат да се считат за $ O (\ влезете N) $ с помощта на парчета дърво - сумата.

В изграждането на дървото на всеки от върха й ще запази размера на съответния интервал (строителството ще се извършва рекурсивно, така че просто да добавите до сумата от два сегмента от дъщерни дружества). След това, всяко искане за сума от сегмента ще бъде разделен на 2 $ \ дневник N $ сегменти, както и намирането на размера на всеки един от тях за $ O (1) $ използване predproschitannye стойност. Така сложността на размера на искането е $ O (\ влезете N) $.

В допълнение към размера на искания към парчетата дървесина също може да направи искания за промяна на отделните елементи (модификация). Имайте предвид, че чрез промяна на един от елементите на сумата ще се промени в най-отгоре на всяко ниво на сегментите на дърветата (които включват този елемент). Преизчислени стойности (отново рекурсивно) само в тези върхове. Така модификация сложност искане равно на височината на дървото, или $ O (\ влезете N) $.

За изпълнение на искането и на размера на модификация на пропускане на заявката дърво се осъществява чрез използване на същия алгоритъм на базата на DFS. Нека границите на нашата молба $ [L; R] $ (в случай на искане модификация $ L = R $), и границата на сегмент, съответстващ на текущия връх $ [TL; TR] $. В зависимост от относителното положение на тези граници, има три варианта алгоритъм:

Настоящото сегмент изцяло се съдържа в заявката ($ L \ ле TL; TR \ ле R $).

Ако искането е количеството predproschitannuyu сума за възстановяване на сегмента. Ако това искане модификация, и промяна на размера на елемента Преизчисляване. Детето възли не е необходимо да се понижат.

Сегашната сегмент не е напълно включен в заявката ($ TR

Не е необходимо действие, просто оставете функцията. Ако искането е размерът на възстановяване на $ 0 $.

Текущ сегмент е частично включена в искането.

Обадете се на функцията рекурсивно към двете дъщерни сегменти. Ако това е сумата на искането, да възстанови сумата от двете стойности, получени. Ако това искане модификация, преизчисляване на стойността на сумата от текущия сегмент (тъй като може да са се променили).

Ще означаваме тези опции съответно зелени, червени и жълти. Тогава количеството на искане за сегмент $ [1; 11] дължина $ масив $ 13 $ ще се обработват както следва: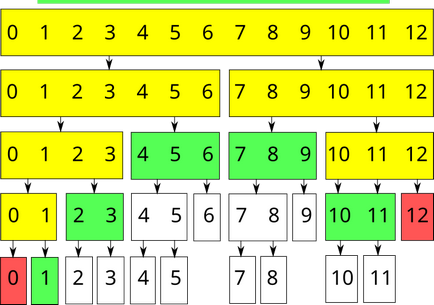

заявка за промяна $ 4 $ тия елемент:

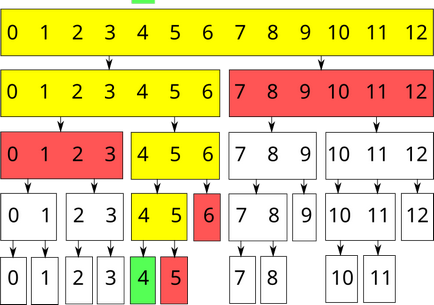
Изпълнение на дължини на дървото, за да се намери сумата

Пълна двоично дърво настоящото, като в лекция за купчината и с набор от формули преход $ л = 2v $ и $ г = 2v + 1 $. За да се избегне всички възможни парчета размер преливане от дървен материал за масива от $ п $ елементи са равни на $ 4п $.

Изпълнение на C ++:

Изпълнение на дължините на дърветата, за да търсят най-малко

За да намерите минимум трябва да се промени в предишното изпълнение на само няколко реда:

Дървета сегменти, консерванти всички елементи

За решаването на някои проблеми на върха, която е отговорна за сегмента, трябва да пази всички елементи на този сегмент в реда на сортиране. Може да изглежда, че това ще отнеме твърде много памет, но това не е така. Всеки елемент от масива се съхранява само веднъж на всяко ниво от дървото, от които $ \ дневник п $. Следователно, цялата структура на данните отнема $ O (N \ влезете N) $ памет.

Класически проблем на сегментите на дърветата от този вид е, както следва:

Като се има предвид масив от $ N $ номера, който получава заявки за $ M $. Заявки приеме формата $ (L, R, X) $. За да се отговори на всеки поискване, колко елемента, е по-голям от или равен на $ х $, се съдържа в интервала $ [л; R] $.

За да се реши този проблем ще бъде във всеки възел на дължините на дърветата, за да сортиран станд :: вектор. съдържащ всички елементи на съответния сегмент. За да отговорим на запитването ще използва станд :: LOWER_BOUND. Тя ви позволява да отговори на искането за един връх от $ O (\ влезете N) $, така че общата сложност на отговора на молбата ще бъде равна на $ O (\ влезете ^ 2 N) $.

Изпълнение на C ++:

Ако тези проблеми могат да бъдат изменение на елементи, вместо STD :: вектор трябва да се съхранява станд :: MultiSet. който ви позволява бързо да добавяте или изтривате елементи. Но в този случай ние не можем повече да реагира редица елементи, като итератори станд :: MultiSet не може да отнеме един от друг.

Дървени парчета с помощта на мащабна актуализация. непоследователни поддървета

Поради някои модификации сегмент дърво може да изпълнява елементи за актуализация (увеличаване или прехвърляне) на интервали от произволна дължина на $ O (\ влизане N) $. Тази модификация е често срещано явление и може да се реши с помощта на парчета дърво са клас нови задачи.

Идеята е, както следва. Да предположим, че в хода на искането за предоставяне на интервала отидохме до върха, изцяло притежавано от този сегмент. Според логиката, че трябва да се промени стойността в горната част, както и във всички по върховете на своята поддърво. Но сложността на такава операция е неприемливо висока: $ O (N \ влезете N) $.

Вместо това, ние се процедира, както следва: промените стойността на само най-горната част, без да актуализирате своята поддърво (по този начин, в поддървото остарели неправилни стойности вече са съхранени), и не забравяйте, че този връх е некоординирана модификация. В това изпълнение на искането за срещата на върха и поддървото е завършена.

Ако следващи заявки няма да се прилагат по отношение на поддървото с неодобрена модификация, те ще се извършва правилно. Но рано или късно да бъде поискано да се обработват индивидуално за деца възли с непоследователно модификация. В този случай, което правим, е проста: да даде на децата на промяната (само дъщерни върхове, не целия под-дърветата). Сега в началото на тази съгласи и я пусна към несъответствието на детето си. Тази операция се нарича натискане модификация.

Може би, за да придвижи искането изисква единствено дете възли, и с едно натискане ще бъде достатъчно. Ако искането е по-долу от под-дървото, тъй като тя ще настоява промяната на затвора по-ниско и по-ниско. Бутане писти в $ O (1) $ в същото време споделя заявката, така асимптотичния поведение не е засегната.

Например, да предположим, че ние работим с сегменти на дървото, за да се намери сумата от масивна задача. Ние сме присвоил $ [0; 6] $ стойност на $ х $. Променете стойността на сумата в топ отговорен за този сегмент (да го настроите до $ 7х $) и да зададете параметър за връх некоординирано модификация равно на $ х $.

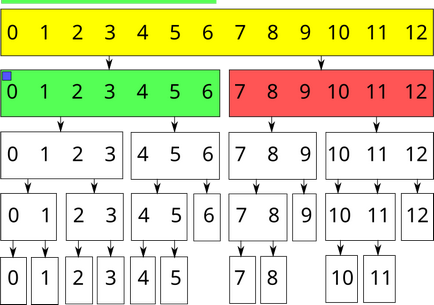
Blue квадрат показва наличието на несъответстващи модификация върхове.

Сега ние ще обработим искане за намиране на сумата от $ интервал [6; 7] $:

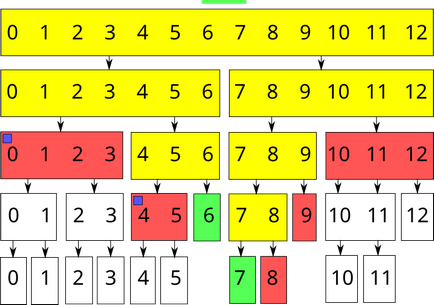
Както можете да видите, несъответствието преминал до $ [0; 3] $ $ и [4; 5] $. Щеше да са преминали и към сегмента $ [6; 6] $, но той все още няма деца възли, така че несъответствието се отстранява.