Формула (1) могат да се прилагат, когато кривата гранична крива трапец, определена от параметрични уравнения
Провеждане на промяната на променлива в интеграла (1) (ако приемем, че когато и ако), получаваме
Ако равнина фигура ограничена по части гладка затворена крива, определена от параметрични уравнения. и когато границата се премества обратно на часовниковата стрелка, площта на фигурата се изчислява по една от формулите:
Пример 7. изчислява площта на фигурата, ограничена от елипса
Първият метод. По отношение на оси на симетрия на елипсата в съответствие с формула (1) могат да бъдат написани
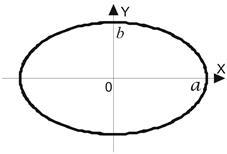
Независимо изчисли интеграл от заместване (както в пример 5).
Вторият метод. Пишем на параметричните уравнения на елипсата:
Долната граница на интеграция съответства на стойността на параметъра. ако. след това. Според формулата (4) намираме
Третият начин. Ако промените настройката от граничните парчета обратно на часовниковата стрелка, като се започне от точката. Например, първата формула (5) намираме
Забележка. Полезно е да се помни, че зоната, ограничена от елипса с полуремаркета оси. определя по формулата
Пример 8. Намерете зоната, ограничена от оста на абсцисата и първата арка Циклоида
Циклоида точка описва окръжност с радиус. подвижен без плъзгане по права линия. Пълен кръг своя страна прави параметъра варира от 0 до. преминаване в същото време в една линия разстояние права. Освен това, ако. след това. ако. след това.
Според формулата (4) намираме
В зоната, ограничена от една арка на Циклоида и оста х е равен на три пъти площта на кръг.
Свързани статии
