1.6 equidecomposability триъгълници. Теорема Bolyaya-Gervin
Много теореми и формули в геометрията доказани чрез рязане форми, и след това изместване на техните части - помни, например, Питагоровата теорема. Ако двете цифри могат да бъдат нарязани на същия набор от части (т.е.. Е. между частите на тези комплекти могат да бъдат настроени към един кореспонденция, в която съответните части са равни), тези цифри се наричат equidecomposable. Equidecomposable фигури, разбира се, равна площ - те имат една и съща област. За полигони, точно обратното е вярно теорема: всеки две полигони на равно и опа. През 1832 г. й доказано унгарски математик Фаркаш Бояй, а година по-късно, но независимо от това, германската GP Gervin. Ключът към доказателството - прекрояване на правоъгълника е показано на фигура 1.40: рязане на "ниска" правоъгълник в два триъгълника и петоъгълник, триъгълници се плъзгат по наклонената раздел линия, които получаваме друг, "висока" правоъгълник.
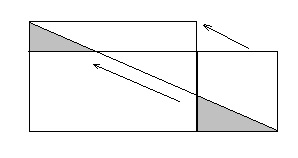
По този начин, на правоъгълника не е трудно да конвертирате почти всеки друг, равен на него - просто трябва да имаме нова кутия е "горе" на оригинала, но не повече от два пъти. Ако съотношението на височината на правоъгълника по-голяма от два (фиг. 1.41, а) "ниска" да "по-висока" от проста трансформация (фиг. 1.41, б) се прилага многократно.
Сега всеки полигон можем да преначертае правоъгълника определена постоянна височина часа. го нарежете на триъгълници, всеки триъгълник превърне в правоъгълник (фиг. 1.42), ние представяме правоъгълници, получени на постоянна височина часа и sostykuem вертикални страни.
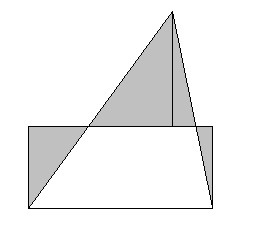
Ако два триъгълника с еднаква площ, кутийките, съответстващи на постоянна височина ч равни. По този начин, тези полигони са опа с една и съща фигура, а от там можем да заключим, че те са и опа заедно.
1.7 съотношението на областта на подобни триъгълници
Теорема 1. Площта на двата триъгълника с Равен ъгъл са като произведения на лица, влизащи в тези ъгли.
Доказателство. Нека триъгълник ABC, и (фиг. 1.43), ъгли А и В са еднакви.
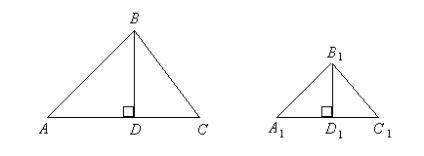
След като прекарва височината и ние имаме:
Триъгълниците и други подобни ( А и А1 = D = D1 = = 0 до 90), обаче; подмяна на втория първата връзка, получаваме:
Теорема 2. Областите на подобни полигони като квадрати са еднакви страни.
Доказателство. 1) Ако - два подобни триъгълници, ъглите на ъглите са, съответно, от друга страна; нека
Приложими към тях предишната теорема:
Но поради сходството на триъгълници следва:
Ето защо, в уравнението (1.14) можем да всеки от отношенията и да се замени с произволен брой връзка (1.15), следователно,
2) Ако (фигура 1.44) -. Две подобен многоъгълник, те могат да бъдат решени в същия брой на еднакво разстояние и на подобни триъгълници.
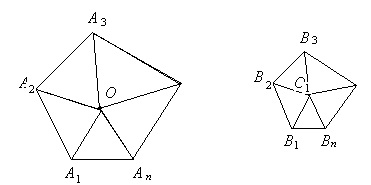
Нека тези триъгълници са:
Според това, което е доказано в първата част на тази теорема, ние получаваме съотношение:
Но поради сходството на полигони трябва да бъде:
Следствие. Квадратни правилни многоъгълници са със същото име като страните на квадрата, или площади apofem радиуси.
1.8Figury с най-голяма площ
1.8.1 Line или правоъгълник
Разглеждане на този елемент се започне с решаването на проблема.
Задача. В съдбовен ден в живота си в слабините премина 40 версти, които ходят по стените на зоната на трапец от 78 квадратни версти. Неговата първоначална цел бе да се отиде на страните на правоъгълник, трапец е включено случайно, в резултат на лошо изчисление. Интересно е да се определи: печалба или той е изчислил неправилно на този сайт не е правоъгълник, трапец? В този случай, той трябва да е получила голяма площ на земя?
Решение. Шунтираните кутии с 40 отвори могат да бъдат много, и всеки от тях има различна област.
Ето някои примери:
14 6 = 84 кв. вентилационни отвори
13 7 = 91 кв. вентилационни отвори
12 8 = 96 кв. вентилационни отвори
11 9 = 99 кв. вентилационни отвори
Ние виждаме, че всички тези лица, които имат една и съща периметъра на 40 версти площ по-голяма от тази на нашето трапец. Въпреки това, тези правоъгълници са възможни с периметър 40 вентилационни отвори, чиито район е по-малък от този на трапеца:
18 2 = 36 кв. вентилационни отвори
19 1 = 19 кв. вентилационни отвори
19,5 0,5 = 9,75 квадрат. вентилационни отвори.
Следователно, въпросът на проблема е невъзможно да се даде еднозначен отговор. Има кутии с по-голяма площ от трапеца, но има и по-малко, а в същото периферията. Но вие може да даде много категоричен отговор на въпроса: кой от всички правоъгълни форми на с даден периметър обхваща най-голяма площ? Сравнявайки нашите кутии, ние се отбележи, че по-малката разлика в дължината на страните, площта на правоъгълник по-дълго. Естествено е да се заключи, че когато разликата въобще не е така. Д. Когато правоъгълника стане квадрат площ от цифрата ще достигне максималната си стойност. След това ще се равнява на 10 10 = 100 кв. вентилационни отвори. Лесно е да се види, че този квадрат е наистина превъзхожда в областта на всеки правоъгълник е равна на периметъра на него. Pahomu трябва да върви от двете страни на площада, за да получите максимална площ на земя - 22 квадратна миля повече, отколкото той може да достигне.
1.8.2Zamechatelnoe квадратен имот
Забележителна собственост на площада - затворена в нейните граници най-голяма площ в сравнение с всички останали квадратчета от един и същи периметър. Ние даваме строга доказателство.
Означаваме периметъра на форма правоъгълна през R. Ако вземете квадрат с периметър, всяка страна трябва да бъде. Ще докажем, че скъсяването на едната страна на това, че тя да б в същото удължаване на съседните страни, ние получаваме правоъгълник от същия периметър с него, но по-малка площ. С други думи, да се окаже, че площта на квадрат по-голяма от площта на правоъгълник:
От дясната страна на това неравенство е, а след това на целия израз е: или.
Но последното неравенство е очевидна: площада на всяко количество, положително или отрицателно, е по-голяма от нула. Вследствие на това е вярно и оригинален равенство, което ни доведе до това.
По този начин, на площада има най-голяма площ на всички правоъгълници със същия периметър.
Това следва от факта, че на всички правоъгълни форми с една и съща област на площада има най-малък периметър. Това може да се види от следната мотивите. Да приемем, че това не е вярно и че има правоъгълник с равен А., който е квадрат в района има периметър по-малък от него. След това, чрез изтегляне на квадрат със същия периметъра като тази на правоъгълник А. получаване на квадрат с по-голяма площ, отколкото в А. и следователно по-голяма от тази на квадратен В. В резултат на това е установено, че един квадратен С има периметър по-малък от квадратен В. а площта е по-голяма, отколкото той. Очевидно е невъзможно: време квадратен страна с по-малък от страна на площада и района V. трябва да бъде по-малко. Така че това е невъзможно да се признае съществуването на правоъгълник, който в същия район има периметър по-малък от площада. С други думи, на всички правоъгълници със същата площ има минимален периметъра на квадрат.
Познаването им свойства квадратен помогна Pahomu правилно изчисляване на силите и да получите правоъгълна област на най-голямата област. Знаейки, че той може да премине на ден, без стрес, например, 36 вентилационни отвори, той ще отиде по протежение на границата на квадрат със страна 9 мили, а вечерта ще бъде собственик на сайта в 81 квадратна миля - 3 квадратна миля повече, отколкото той получил фатален натоварвания. От друга страна, ако тя е била ограничена предварително за всеки конкретен район на правоъгълната зона, например, 36 квадратни версти, това може да се постигне в резултат най-малко разходи на енергия, да не преминат границата на квадрат чия страна - 6 дюзи.
Свързани статии
