Коничната секция. или конична [1]. - точката на пресичане на равнина с кръгов конус. Има три основни вида конични сечения: елипса. парабола и хипербола. В допълнение, има изродени раздел: точка. и двойка прави линии. Кръгът може да се разглежда като специален случай на елипса.
Конусни части могат да бъдат получени като пресичането на равнината с двустранен конус
Ако самолетът преминава през началото. Оказва дегенерат секция. В случай на не-дегенерат,
- ако рязане равнина пресича всички генератори на точките на конус в една от неговите кухина получаване на елипса,
- ако пресичащи равнина е успоредна на тангенциалната равнина на конуса, парабола,
- ако равнина раздел пресича както кухината на конуса, получаваме хиперболата.
Уравнението на кръгов конус квадратен следователно всички конични секции са quadrics. и всички quadric равнина са конични части (въпреки че две успоредни линии образуват дегенеративен quadric, които не могат да бъдат получени като част на конуса, но все пак обикновено се счита за "дегенеративен конична").
Конично раздели са били известни гръцки математика.
Най-пълни са творби, посветени на тези криви са "конично раздели" Аполоний Пергски (около 200 г. пр.н.е.. Д.). Очевидно е първият за описване на огнища на елипсата и хипербола [2]: 41.
Papp Александрия описан за първи път фокус на параболата и производни с обща формула за конично сечение като локус. за които съотношението на разстоянието до точката на фокусиране и постоянен директриса [2]: 48.
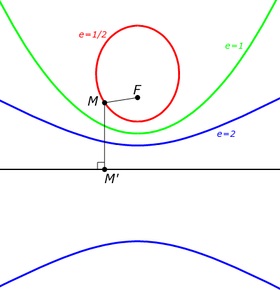
Елипса (д = 1/2). парабола (д = 1) и хипербола (д = 2) с фиксиран фокус F и директриса.
Всички не-дегенеративни конични секции, в допълнение към кръг. Това може да бъде описано както следва:
Ние избираме точка F на самолета и ред г и определяне на реално число д ≥ 0. Тогава мястото на точки. за което разстоянието до точката F и линия г до Д в различни времена, коничната секция. Точка F е във фокуса на конично сечение, директна г - директорка. броят на д - ексцентричност.
В зависимост от ексцентричност, вие получавате:
Изместването се отнася до параметрите на конус и разположени по отношение на намаляване на равнината на конус ос на следната формула [3]: 46.47:
Тук ψ - ъгъл на рязане на равнината на оста на конуса, φ - ъгълът между образуващата и оста на конуса, равна на половината ъгъл на конуса. От тази формула се вижда, че конуса пресичаща равнината може да се получи с всеки ексцентричност елипса, парабола, хипербола и може да се получи само, така че ексцентричност не е повече от 1 защото φ >>. Тази максимална стойност се достига при дадено напречно сечение на конуса от равнина, успоредна на оста си.
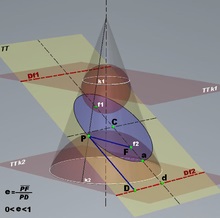
Елипса (син) като конично сечение, разделяне dandelin сфери; елипса директорка (DF1 и Df2), неговият фокус (F1 и F2) и ексцентричност (д)
Някои важни свойства на конични части се получават от това, две топки, свързани с конични и конусни - топки Dandeli. Например, с тяхна помощ зададете геометрична смисъла на фокус, а директриса коничен ексцентричност [3]: 46.47.
- След всички пет точки в равнина, всеки три от които са колинеарни, е възможно да се проведе само с конично сечение.
- Изместването на две не-дегенеративни конични части съвпадат ако и само ако те могат да бъдат превърнати едно в друго чрез трансформация сходство.
- Affine трансформации запазват само знака на ексцентричност, т.е. от гледна точка на афинна геометрия на има само три различни не-дегенеративни конични части: елипса, парабола и хипербола.
- Всички не-дегенеративни конични секции са неразличими в проективна геометрия.
декартови координати
А х 2 + B + C х Y Y 2 + D х + у E + F = 0. + Bxy + Су ^ + Dx + Ey + F = 0,>
Тя определя типа на конично сечение.
- Ако дискриминантата е по-малко от нула, то тогава е елипса. точка или празното множество.
- Ако дискриминантата е нула, то тогава е парабола. с права или двойка успоредни линии.
- Ако дискриминантата е по-голяма от нула, а след това е хипербола или двойка пресичащи се линии
полярна координатна
В полярни координати (ρ. Θ). центрирана в една посока фокус и нула по главната ос, коничната част е представена от уравнението
където е е ексцентричност и л константа.
В класическата механика, траекторията на свободното движение на сферични обекти във вакуумна е обект на едно от приложенията, закона за обратна пропорционалност - закона за всемирното привличане. и следователно е един от наклон на кривата - парабола, хипербола, елипса или права линия. Планетарни орбити - елипси траектория комети - елипси, хиперболи [4] или "почти параболична" [5] (виж също небесната механика.), Траекторията на полета изстрел с изключение на въздух въздействието - (. Виж също балистика) елипса дъга.
Свързани статии
