инфлексна точка

графиката на инфлексната точка

Определение. от точката на графика се нарича инфлексна точка на тази графика, ако съществува квартал на хоризонталната ос, в рамките на който графиката на ляво и в дясно от точката, има различни посоки изпъкналост.

Ако функцията е диференцируема в точката и околностите, за геометрично Това означава, че графиката на комбинация в близост до единия край на допирната точка на друг (фиг. 3).

Ако функцията е непрекъсната в. диференцируема в квартала. с изключение на точката. и. графиката на функцията в близост до точката, разположени на противоположни страни на вертикална тангента (фиг. 4).

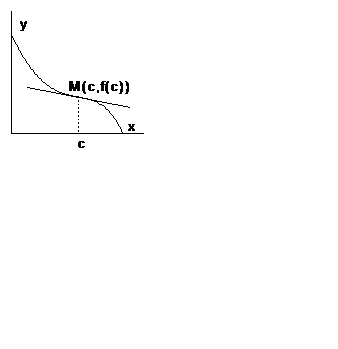
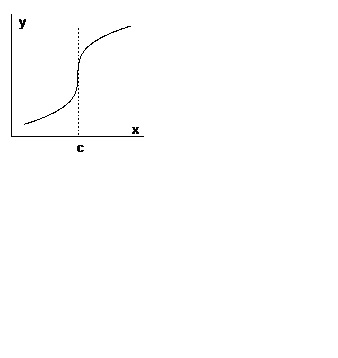
Теорема 3 (необходимо условие за съществуването на инфлексната точка). Да предположим, че функцията е непрекъсната в точката на втората производна. След това, ако точката е точка на инфлексия на графиката, след това.

Имайте предвид, че състоянието е необходимо, но не достатъчно условие на инфлексия на графиката на точката. Помислете, например функцията. Вторият производно на тази функция. нула цяло. Въпреки това, на цялата реална ос. Следователно навсякъде в графиката на тази ос е изпъкнала надолу, и точката не е точка на инфлексия.

Теорема 4 (достатъчно условие за инфлексната точка). Ако функцията е диференцируема в точката. два пъти диференцируема в околност на точката. с изключение, може би, най-много точки и втората производна промени подписват при преминаване през точката на спора. точката е инфлексна точка на графиката на функцията.

Имайте предвид, че ако функцията е непрекъсната в. два пъти диференцируема в околност на точката. с изключение на точката. и има допирателна в точката (поне успоредно на оста), след твърдението на теоремата 4 също е вярно.

Пример 1. Виж на инфлексна точка на графиката на функцията.

Намираме производни предварително определена функция:

става нула в точките. и промени да подпишат, когато преминават през тези точки. Следователно, точките и са точките на инфлексия на функциите на графиката. Имайте предвид също, че в интервалите и. следователно, графиката на функцията е изпъкнала нагоре. В интервал. и функция график има изпъкналост, насочена надолу.

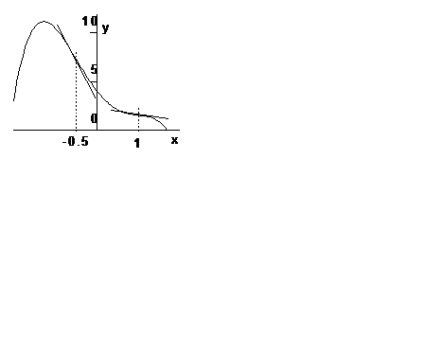
Пример 2. Виж точката на огъване на функциите на графиката.

Тази функция е непрекъсната по цялата реална ос и има

крайния втората производна навсякъде в брой линия, с изключение на най-важното. И когато. и кога. В точката на първата производна на функцията не е дефинирана. Тъй като. графиката на функцията е точка (1,2) вертикална тангента. От втората промени деривативни подписват при преминаване през точката. точката (1,2) е инфлексната точка.

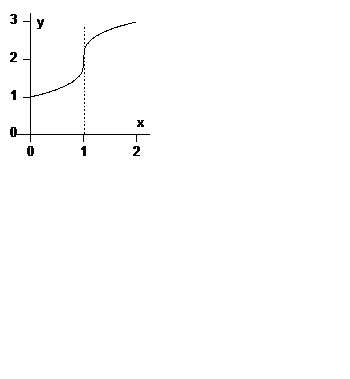
Посоката на графиката на изпъкналост

Нека функцията е диференцируема в даден момент от време. т.е., че има във всяка точка на интервала краен производно. Тогава там е допирателната към графиката на функцията. минаваща през всяка точка на графиката. където тази допирателна не е успоредна на оста.

Определение. Казват, че графиката на интервала е изпъкнала надолу (нагоре), ако графиката на тази функция не е по-малко от (не повече от) някоя от нейните допирателната.

Фиг. 1 показва графика на функция, която е изпъкнала надолу, както е показано на фиг. 2 - изпъкнала нагоре.

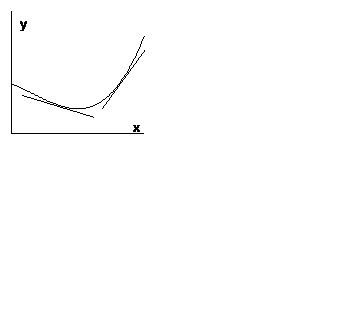
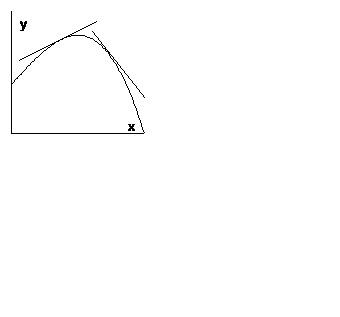
Теорема 1. Ако функцията е интервалът приключва, когато вторият производно и това производно е неотрицателно (не-позитивни) в този диапазон, графиката на функцията е изпъкналост на интервал насочена надолу (нагоре).

Теорема 2. Да приемем, че втората производна е непрекъсната и положителен (отрицателен) в точката. тогава съществува околност на точката. в който функция графиката е изпъкнала надолу (нагоре).

Свързани статии