Силови функции, областта на определение.
Момчета, последния урок, ние се научат как да работят с номера с рационален показател. В този урок ще разгледаме функцията за сила и само в случая, когато степенният показател е рационално.
Ще разгледаме функцията на форма: $ Y = х ^> $.
Помислете първо функцията, в която експонат $ \ Frac> 1 $.
Да предположим, че са дадени специфична функция $ Y = х ^ 2 * 5 $.
Според определението, което сме дали в предишния урок: ако $ x≥0 $, че е домейнът на нашата функция - 0 лъч $ [+ ∞) $.
Стойностите в таблицата.
Нека се обърнем към случая, когато експонентата - подходяща фракция (т.е., когато числителят е по-малко от знаменател).
Да сравним три мощност функция: $ у = х ^ 2 $; $ Y = х ^ $; $ Y = X ^ 3 $.
Броят 2.5 е между 2 и 3, след това изглежда, че графиката на нашата функция ще бъде между съответните графики. Сравнете стойностите за различните функции на х.
1. Ако $ 0
На земята под диаграмата за случай $ 0Свойства на силови функции
Свойства на функция $ Y = х ^> $, $ (т> п) $:
1. $ D (у) = [0 + ∞) $.
2. Има ли още или странно.
3. Отглеждане на $ [0 + ∞) $.
4. Не, ограничена по-горе, оградена по-долу.
5. Най-голямата ценност не е налице, най-ниската стойност е нула.
6. непрекъснато.
7. $ Е (е) = [0; + ∞) $.
8. изпъкнала надолу.
Графиката на $ у = х ^> $, (т> п) $ $ е подобен на графиката на $ у = \ SQRT [п] $. Нека схематично изобразяват нашия график функция. 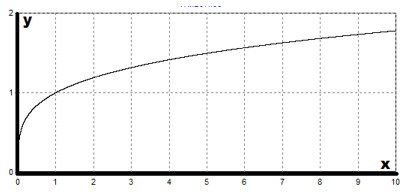
Свойства на функция $ Y = х ^> $, 0 $ $ 0 и г - всяко рационално число, тогава производното на мощност функция $ у = х ^ R $ се изчислява както следва: $ Y '= R * х ^ $.
Пример. Намерете най-голямата и най-малката стойност на функцията $ у = х ^> $ от сегмента:
а) $ [1, 16] $,
б) $ (2,10) $
в) на лъч $ [9 + ∞) $.
Решение.
Експонатът на нашата функция е положителна. След това погледнете в свойствата на нашата функция, ние виждаме, че тя расте в цялата област. Това означава, че тя достига максимални и минимални стойности в краищата на предварително определени дължини (ако е определено в тези точки).
а) $ y_ = 1> = $ 1; $ Y_ = 16 ^> = (\ SQRT) ^ 5 = 4 ^ 5 = 1,024 $.
б) най-високите и най-ниските стойности на функцията на този интервал не е, както ни е било дадено отворен интервал, и 0 и 4, тази празнина не принадлежи.
в) най-голямо значение има.
$ Y_ = 9 ^> = \ SQRT = (\ SQRT) ^ 5 = 3 ^ 5 = $ 243.
Пример. Виж най-голямата и най-малката стойност на функцията: $ у = \ fracx ^> - \ fracx ^ 4 $ в сегмент $ [1, 9] $.
Решение.
Момчета, помниш ли как ние открихме най-голямата и най-малката стойност на функцията на сегмента в 10 клас?
Точно така, ние сме използвали производно. Нека да решим нашия пример и повторете алгоритъма за търсене на най-малката и най-голямата стойност.
1. Да се намери производната на дадена функция:
$ Y '= \ Frac * \ fracx ^> - х ^ 3 = 8x ^> - х ^ 3 = 8 \ SQRT-х ^ 3 $.
2. производно съществува в целия домен на оригиналната функция, а не критични точки. Намираме стационарни точки:
$ Y '= 8 \ SQRT-х ^ 3 = 0 $.
8 $ * \ SQRT = х ^ 3 $.
$ 64x ^ 3 = х ^ 6 $.
$ X ^ 6-64x ^ 3 = 0 $.
$ X ^ 3 (х ^ 3-64) = 0 $.
$ X_1 = 0 $ и $ x_2 = \ SQRT [3] = 4 $.
Задайте сегмент принадлежи само на едно решение x_2 = $ 4 $.
Ние се изгради една маса от ценности на нашата функция в крайните точки и в екстремум:
Отговор: $ у _ = - 862,65 $ от $ х = $ 9; $ Y_ = 38,4 $ от $ х = 4 $.
Пример. Решаване на уравнението: $ х ^> = 24 х $.
Решение. Графиката на $ Y = х ^> $ увеличава, и графиката на функция у = $ 24 $ намалява. Момчета, ние ви да знаят: ако една функция се увеличава и другите намалява, а след това те се пресичат само в една точка, така че ние имаме само едно решение.
Забележка:
8 $ ^> = \ SQRT [3] = (\ SQRT [3]) ^ 4 = 2 ^ 4 = 16 $.
8,24 $ = 16 $.
Това е, когато $ х = 8 $ имаме истинско равенство $ 16 = $ 16, това е решение на нашето уравнение.
Отговор: $ х = $ 8.
Пример.
Построява се графика на функцията: $ у = (х-3) ^ \ Frac + 2 $.
Решение.
График на нашата функция е получена от графиката на $ у = х ^> $, компенсира това с 3 единици в дясно и 2 единици до.
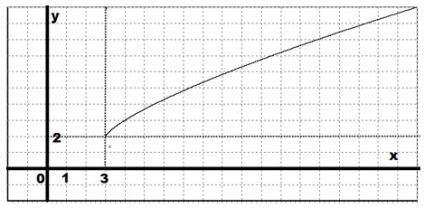
Пример. Уравнението на допирателната към $ у = х ^> $ на 1 $ = $ х.
Решение. Уравнението на допирателната се определя по известен формула:
$ Y = F (а) + F '(а), (х-а) $.
В нашия случай долара = 1 $.
$ F (а) = F (1) = 1> = 1 $.
Нека да намерим производната:
$ Y '= - \ fracx ^> $.
Изчисляваме:
$ F '(а) = - \ Frac * 1 ^> = - \ Frac $.
Нека да намерим уравнението на допирателната:
$ Y = 1 \ Frac (х-1) = - \ fracx + 1 \ Frac $.
Отговор: $ у = - \ fracx + 1 \ Фрак $.
Задачи за независим решение
1. Намерете най-голямата и най-малката стойност на функцията: $ Y = х ^ \ Фрак $ от сегмента:
а) $ [1, 8] $.
б) $ (4,50) $.
в) на лъч $ [27 + ∞) $.
2. Виж най-голямата и най-малката стойност на функцията $ у = \ fracx ^> - х $ на сегмент $ [1, 27] $.
3. решаване на уравнението: $ х ^> = 18 х $.
4. Конструкция на графиката на функция: $ Y = (х + 1) -> 1 $.
5. Създаване на уравнението на допирателната към $ у = х ^> $ на 1 $ = $ х.
Добави коментар
Свързани статии
