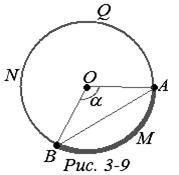
Да предположим, че по-малко от полукръг, и следователно, г (А, В) - дължината на дъгата. Нека стойност централен ъгъл АОВ, въз основа на дъгата AMB и чрез R (А, В) - дължината на сегмента AB. Както е известно,

(. Фигура 3-9) Други въпроси, ние откриваме:

От формулите (1), (2) следва:

3. движение на сферата е всяко изометричен картографиране на сферата върху себе си, т.е.. Д. карта е. S®S, което отговаря на условието: независимо от точка А и сфери, г (A, B) = г (F (А), F (В)). От (3) следва, че в този случай R (A, B) = R (F (А), F (В)). Следователно, всяко движение на сфера е S се генерира от интервал движение f0, където f0 (О) = О. Обратно, всяко движение g0 пространство, оставяйки точка О неизменна на генерира определено движение на сферата S.

От това ние заключаваме, че множеството от движения на сфера S е група, която е изоморфни до подгрупа h0 неподвижна точка О в групата на движения.

Две парчета F, F 'Ì S е еднакви или равно на, ако има движение на сферата S, който носи една от тези фигури в друг. Вследствие на фигура F, F ' Ì S са еднакви, ако те Н0 - еквивалент.

4. Вземете върху сферата S три точки A, B, C не се намира по една и съща голяма кръга. Те определят три на полусферата, всеки от които включва точки А, В и С, два от тези точки принадлежат към ръба на полукълбо. Пресечната точка на тези три полукълба нарича сферичен триъгълник с върха А, В, С Arc AB, BC, AC големи кръгове (по-малко от полукръг), наречена партия на сферичен триъгълник ABC.

Нека ABC - сферичен триъгълник, а = г (В, С), б = г (А, С), с = г (А, В) - дължината на своите страни, а, б, г, съответно ъгли ВОС АОС и АОВ.

Нека докажем синусова теорема за сферични триъгълници.

Теорема. Нека а = г

Тя може да се докаже, че следното уравнение, което изразява косинус теоремата за сферичен триъгълник ABC на:

Можем също така да докаже, че ABC сферична област триъгълник, се изчислява по формулата

където - т.нар излишък сферичен триъгълник. Тъй SABC> 0 пространство, след това от уравнение (8) следва, че е> 0, R. F .. Така, сумата от ъглите на всеки сферичен триъгълник е по-голяма стр. Това е - значителна разлика в геометрията на сферата както на геометрията на Евклид равнина и геометрията в равнината Lobachevskii

Поанкаре модел на хиперболична геометрия. (Френският учен Анри Поанкаре (1854-1912) - най-големият математик модел, описан по-късно бе предложена им през 1882 г. ..) Ролята на самолета Лобачевски полуотворени; ролята на директен работи съдържа полукръг центриран върху ограничаване на преките лъчи и перпендикулярна на тази линия. Размяна на ролите наслагвания работят на състав в сравнение с тези полукръгове и отражения в гредите. Всичко Аксиома Euclidean геометрия се извършват, с изключение на аксиома паралел (Фиг. 4-1, както и), по този начин в този модел се извършва Lobachevskian геометрия.

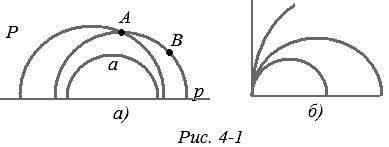
Ние опишем модела по-подробно и шоу каза. Ние приемаме по обичайния евклидовата равнина всяка една линия, р и отворен половин линия р Р. ограничено той се нарича гранична линия. полуравнина P ще играе ролята на самолета Лобачевски; ние го наричаме "равнина" в кавички. Точки в модела ще бъде точката на тази "равнина", т.е.. Е. R. За половин равнина "директно" в модела приема, от една страна, се съдържа в Р полукръг, чиито центрове лежат на гранична линия (Фиг. 4-1, а). "Cut" в модели AV - е дъга от полукръг с краищата А, Б.

Ще подчертая, че в края на "сегмент" не може да бъде в края на полукръг, представляващи права; нейните краища се отстраняват заедно с гранична линия; "Самолет" - е открит половин самолет. Точка "директно" е общ произход на двата "греди" - две полукръгли арки (с изключение на краищата). "Ъгъл" се нарича фигурата на двете греди "" с общ произход, не се съдържат в "директен" (Фиг. 4-1, както и).

В допълнение към тези "преки" има "пряка" - на половин линии, перпендикулярни на граничната линия. Те са в замисъла на полукръговете (Фиг. 4-1, В). Когато центъра на полукръга се отстранява от граничната линия, и полукръга преминава през дадена точка, то се "изправи" и границата отива в половината. Ето защо, ние ще продължим да мислим за тези полу-линии сред "пряка" модела като полукръгове като "полукръга на безкраен радиус." Това ще позволи да се направи без скучни резерви по отношение на тези две, които, обаче, трябва да са наясно с тази конвенция и да бъде готов да се провери за одобрение на такива "полукръгове." ( "Cut" на "прав" - това е обичайната интервал, и "лъчи" - конвенционален греда, а другият -., С изключение на краищата, нарязани на границата)

Нека сега разгледаме в този модел са аксиоми, които не се включват в концепцията за равенство на сегменти и ъгли.

Аксиома паралелно изправяне се отнася до такива аксиоми. В този модел, то очевидно не притежава: през точка А не да лежи на "Директно" и преминава безкраен брой "директно", но нямат обща точка (фигура 4-1, както добре.).

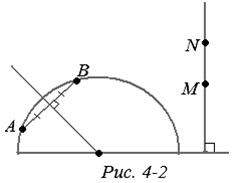
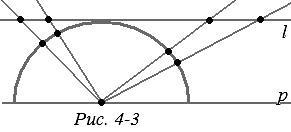
Всички останали аксиоми, говорейки за местата за връзка и сегменти, или точки и линии, взаимното положение на точки и линии се изпълняват. Например, на фиг. 4-2 посочено сегмент строителство данни завършва. След това взимаме полукръг, е "директен" в този модел. Ние се направи линия л, отнасящи се до този полукръг и успоредно на граничната линия. Ние проектира полукръга от центъра на линия L права (Фигура 4-3). Ние се получи едно към едно, запазването на реда на точките, съответствието между точките на линията и половин окръжност, т.е.. Д. "директен" модел. Всички имоти са изразени в аксиоми, са едни и същи. Те също така извършва при половината очевидно, представлява "директен" модел. Аксиома разделяне равнина се осъществява също. "Директно" - полукръг - разделя равнината на две части - вътрешни и външни. Това ще бъде "полуравнина" в нашия модел. От една до друга, че не може да отиде във всяка дъга без да пресичат ги разделите "направо" - полукръг.